题目内容
13.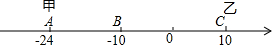 已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,若甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,若甲的速度为4个单位/秒,乙的速度为6个单位/秒.(1)问甲、乙在数轴上的哪个点相遇?
(2)问多少秒后,甲到B的距离为6个单位?
(3)若甲到B的距离为6个单位时,甲掉头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点,若不能,请说明理由.
分析 (1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;
(2)分点A不到B之前,点A到B之后两种情况,列出方程解答即可;
(3)分两种情形讨论说明即可.
解答 解:(1)设x秒后甲与乙相遇,则
4x+6x=34,
解得x=3.4,
4×3.4=13.6,
-24+13.6=-10.4.
故甲、乙在数轴上的点-10.4相遇;
(2)设a秒后,甲到B的距离为6个单位,
A、B之间的距离为14,
当点A不到B之前,4x+6=14,解得x=2;
点A到B之后,4x-14=6,解得:x=5;
答:2秒或5秒后,甲到B的距离为6个单位;
(3)当甲,乙各走5秒时甲在-4处,乙在-20处,且甲速小于乙速,所以永不能相遇.
当甲,乙各走2秒时,甲在-I6处,乙在-2处,两者相距14,所以14÷(6一4)=7秒后乙追上甲,相遇点为6x7+2=44,即-44处相遇.
点评 此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.本题在解答第二问注意分类思想的运用.

练习册系列答案
相关题目
5.计算(-4)2×$\frac{1}{2}$的结果是( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
3.下列计算正确的是( )
| A. | x5-x4=x | B. | 23=6 | C. | -(2x+3)=2x-3 | D. | -x3+3x3=2x3 |
 如图,在平面直角坐标系中有一个Rt△OAC,其中∠ACO=90°,∠CAO=30°,OC=3,将该三角形沿直线AC翻折得到△BAC.一动点P从点O出发,沿折线O→A→B的方向以每秒2个单位的速度向B运动,设运动时间为t(秒).当t=1或5时,△ACP的面积为△AOB面积的$\frac{1}{3}$.
如图,在平面直角坐标系中有一个Rt△OAC,其中∠ACO=90°,∠CAO=30°,OC=3,将该三角形沿直线AC翻折得到△BAC.一动点P从点O出发,沿折线O→A→B的方向以每秒2个单位的速度向B运动,设运动时间为t(秒).当t=1或5时,△ACP的面积为△AOB面积的$\frac{1}{3}$. 有理数在数轴上的对应点位置如图所示,化简:|a|+|a+b|-2|b-a|.
有理数在数轴上的对应点位置如图所示,化简:|a|+|a+b|-2|b-a|. 如图,在△ABC中,∠A=60°,DE∥BC且BD平分∠ABC,CD平分∠ACB,∠EDB=20°,求∠ABC和∠ACB的度数.
如图,在△ABC中,∠A=60°,DE∥BC且BD平分∠ABC,CD平分∠ACB,∠EDB=20°,求∠ABC和∠ACB的度数.