题目内容
3. 如图,在平面直角坐标系中有一个Rt△OAC,其中∠ACO=90°,∠CAO=30°,OC=3,将该三角形沿直线AC翻折得到△BAC.一动点P从点O出发,沿折线O→A→B的方向以每秒2个单位的速度向B运动,设运动时间为t(秒).当t=1或5时,△ACP的面积为△AOB面积的$\frac{1}{3}$.
如图,在平面直角坐标系中有一个Rt△OAC,其中∠ACO=90°,∠CAO=30°,OC=3,将该三角形沿直线AC翻折得到△BAC.一动点P从点O出发,沿折线O→A→B的方向以每秒2个单位的速度向B运动,设运动时间为t(秒).当t=1或5时,△ACP的面积为△AOB面积的$\frac{1}{3}$.
分析 首先求得OA=6,利用翻折得出AB=6,进一步分两种情况:当P点在OA上和P点在AB上两种情况探讨,根据“△ACP的面积为△AOB面积的$\frac{1}{3}$”,列出方程求得答案即可.
解答 解:∵∠ACO=90°,∠CAO=30°,OC=3,
∴OA=6,AC=3$\sqrt{3}$,
∵沿直线AC翻折得到△BAC,
∴AB=6,
如图,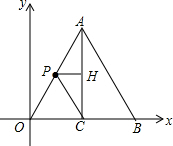
当P点在OA上时,AP=6-2t,PH=$\frac{1}{2}$AP=3-t,
$\frac{1}{2}$×3$\sqrt{3}$×(3-t)=$\frac{1}{3}$×$\frac{1}{2}$×6×3$\sqrt{3}$
解得:t=1;
如图,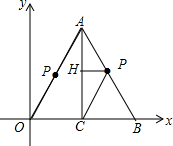
当P点在AB上,AP=2t-6,PH=$\frac{1}{2}$AP=t-3,
$\frac{1}{2}$×3$\sqrt{3}$×(t-3)=$\frac{1}{3}$×$\frac{1}{2}$×6×3$\sqrt{3}$
解得:t=5;
所以当t=1或5时,△ACP的面积为△AOB面积的$\frac{1}{3}$.
故答案为:1或5.
点评 此题考查翻折的性质,含30°角的直角三角形的性质,三角形的面积,利用三角形的面积建立方程是解决问题的关键.

练习册系列答案
相关题目
14.已知直线l,在l上取一点A,经过点A与l相切且半径为5cm的圆有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列方程中是一元二次方程的是( )
| A. | x2+1=0 | B. | y2+x=1 | C. | 2x+1=0 | D. | x+$\frac{1}{x}$=1 |
8.下列关系式中,属于二次函数的是(x为自变量)( )
| A. | y=ax2+bx+c | B. | $y=\sqrt{{x^2}-1}$ | C. | $y=\frac{1}{x^2}$ | D. | $y=\frac{1}{8}{x^2}$ |
15.若132x=64,则13-x=( )
| A. | -$\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | $\frac{1}{80}$ | D. | $\frac{1}{512}$ |
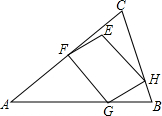 如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.
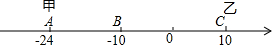 已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,若甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,若甲的速度为4个单位/秒,乙的速度为6个单位/秒.