题目内容
定义一种新运算:观察下列各式:
1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4=5×4+4=24 ;4⊙(-3)= 4×4-3=13
(1)请你想一想:a⊙b=___________;
(2)若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ;
(3)若a⊙(-2b) = 4,请计算 (a-b)⊙(2a+b)的值.
(1)
 (1分) (2) (1分) (3)6(3分)
(1分) (2) (1分) (3)6(3分)
【解析】
试题分析:(1)观察前面的例子可得a⊙b=
 ;(2)根据定义a
;(2)根据定义a ⊙b=
⊙b=
 ,b⊙
,b⊙ a=4b+a,因为a≠
a=4b+a,因为a≠ b,所以a⊙b b⊙a;(3)根据定义先将a⊙(-2b) = 4化简得出a,b,代入(a
b,所以a⊙b b⊙a;(3)根据定义先将a⊙(-2b) = 4化简得出a,b,代入(a -b)⊙(2a+b)计算.
-b)⊙(2a+b)计算.
试题解析:(1)观察前面的例子可得a⊙b=
 ;(2)根据定义a⊙b=
;(2)根据定义a⊙b=
 ,b⊙a=4b+a,因为a≠b,所以a⊙b b⊙a;(3)因为a⊙(-2b) = 4,所以4a-2b=4,所以2a-b=2,(a-b)⊙(2a+b)=4(a-b)+ (2a+b)= 4a-4b+ 2a+b=6a-3b=3(2a-b)=3×2=6.
,b⊙a=4b+a,因为a≠b,所以a⊙b b⊙a;(3)因为a⊙(-2b) = 4,所以4a-2b=4,所以2a-b=2,(a-b)⊙(2a+b)=4(a-b)+ (2a+b)= 4a-4b+ 2a+b=6a-3b=3(2a-b)=3×2=6.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
|


(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线 过点
过点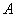 (,
(,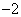 ),
),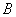 (3,
(3,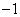 ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
 C外做等边△ABD和等边△ACE.连接BE,CD.请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹)
C外做等边△ABD和等边△ACE.连接BE,CD.请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹)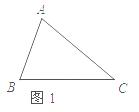

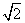 米,AC=AE.求BE的长.
米,AC=AE.求BE的长.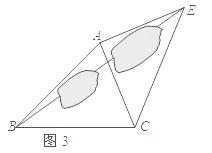
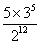 B.
B. C.
C.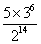 D.
D.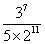
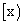 表示大于
表示大于 x的
x的 最小整数,如
最小整数,如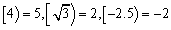 ,现对64进行如下操作:
,现对64进行如下操作: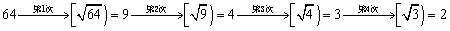 ,这样对64只需进行4次操作后变为2,类似地,
,这样对64只需进行4次操作后变为2,类似地, 最大的是 .
最大的是 . 的两个实数根。
的两个实数根。 的取值范围;
的取值范围; 成立?若存在,求出
成立?若存在,求出 若不存在,请说明理由。
若不存在,请说明理由。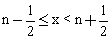 ,则<x>=n。
,则<x>=n。
 ,m为非负整数时,
,m为非负整数时,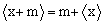 ;
; 的所有非负实数x的值;
的所有非负实数x的值;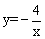 的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】 <y1<y2 B.y1<y
<y1<y2 B.y1<y
 2<y3 C.y3<y2<y1 D.y2<y3<y1
2<y3 C.y3<y2<y1 D.y2<y3<y1 在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是
在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是 中心对称图形的概率为【 】
中心对称图形的概率为【 】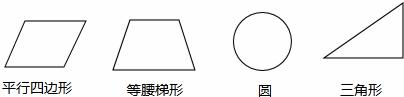
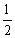 B.
B. 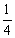
 C.
C. 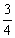 D.1
D.1