题目内容
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
|


(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
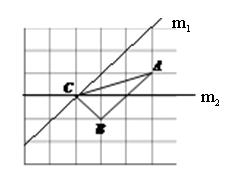
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线 过点
过点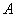 (,
(,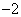 ),
), (3,
(3, ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
(1)见解析;(2)图形详见解析;(3)存在点P(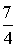 ,-
,-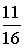 ) 或(-2,-
) 或(-2,-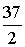 )使S△APC=S△BPC.
)使S△APC=S△BPC.
【解析】(1)分别作AE⊥CD,BF⊥CD,垂足为E,F
∴∠AEP=∠BFP=90°∵P是AB中点, ∴AP=BP又∵∠APE=∠BPF∴△AEP≌△AFP
∴AE=BF,即直线CD是点A、B的一条等距线.

(2)如图,直线m1、m2就是所有的直线
(3)由题意知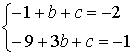 ,得
,得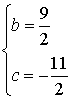 ,∴抛物线为y=-x2+
,∴抛物线为y=-x2+ x-
x-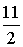
∵S△ APC=S△BPC.,∴A、B两点到直线PC的距离相等
APC=S△BPC.,∴A、B两点到直线PC的距离相等
①当PC∥AB时,计算得直线AB解析式为y= x-
x- ,直线CP解析式为y=
,直线CP解析式为y= x-
x-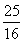
解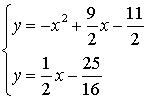 ,得x1=
,得x1=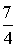 ,x2=
,x2= ;∴点P(
;∴点P(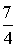 ,-
,-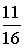 );
);
②当直线CP过AB中点时,易求AB中点E(2,-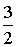 ),直线CE解析式为y=
),直线CE解析式为y=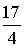 x-1
x-1 0,
0,
解 ,得x1=2,x2=
,得x1=2,x2= ;;∴点P(-2,-
;;∴点P(-2,-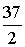 )
)
综上所述存在点P(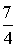 ,-
,-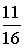 ) 或(-2,-
) 或(-2,-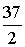 ) 使S△APC=S△BPC.
) 使S△APC=S△BPC.

练习册系列答案
相关题目
 的最小值是 .
的最小值是 .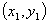 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为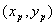 .由
.由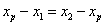 ,得
,得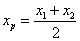 ,同理
,同理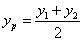 ,所以AB的中点坐标为(
,所以AB的中点坐标为(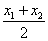 ,
, ).由勾股定理得
).由勾股定理得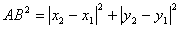 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=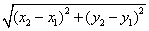 .
. 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.


 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;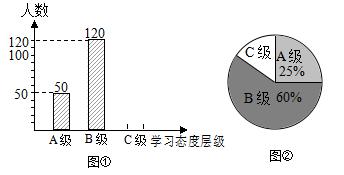

 )(y+
)(y+
 )=1.求证:x+y=0.
)=1.求证:x+y=0. 形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24
形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24 平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.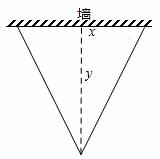
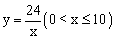 B.
B. 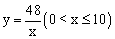
 C.
C. 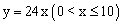 D.
D. 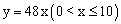
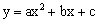 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数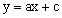 在同一平面直角坐标系中的大致图象是【 】
在同一平面直角坐标系中的大致图象是【 】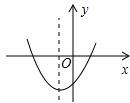
 B.
B.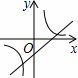

 C.
C. D.
D.