题目内容
18.解方程组:$\left\{\begin{array}{l}{x+3y=1}\\{x^2+xy-6y^2=3}\end{array}\right.$.分析 把x+3y=1化为x=1-3y,代入②,求出y的值,把y的值代入x=1-3y求出x,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{x+3y=1①}\\{{x}^{2}+xy-6{y}^{2}=3②}\end{array}\right.$
由①得,x=1-3y③,
把③代入②得,-5y=2,
解得,y=-$\frac{2}{5}$,
把y=-$\frac{2}{5}$代入③得,x=$\frac{11}{5}$
所以方程组的解为:$\left\{\begin{array}{l}{x=\frac{11}{5}}\\{y=-\frac{2}{5}}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,灵活运用代入法解方程组是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
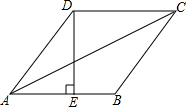 如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.
如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.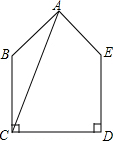 如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17.
如图,面积为72的五边形ABCDE中,BC=DE=7,CD=8,∠BCD=∠EDC=90°,连接对角线AC,则AC+AE的最小值为17. 数学课上,李老师布置的作业是图中小黑板所示的内容,楚楚同学看错了第(2)题※中的数,求得(1)的一个解是x=2,翔翔同学由于看错了第(1)题中※中的数,求得(2)的一个解是x=3,你知道今天李老师布置作业的正确答案吗?请你解出来?
数学课上,李老师布置的作业是图中小黑板所示的内容,楚楚同学看错了第(2)题※中的数,求得(1)的一个解是x=2,翔翔同学由于看错了第(1)题中※中的数,求得(2)的一个解是x=3,你知道今天李老师布置作业的正确答案吗?请你解出来?