题目内容
20．
如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF的度数为（ ）| A． | 48° | B． | 36° | C． | 30° | D． | 24° |
分析 根据角平分线的性质可得∠DBC=∠ABD=24°，然后再计算出∠ACB的度数，再根据线段垂直平分线的性质可得BF=CF，进而可得∠FCB=24°，然后可算出∠ACF的度数．
解答 解：∵BD平分∠ABC，
∴∠DBC=∠ABD=24°，
∵∠A=60°，
∴∠ACB=180°-60°-24°×2=72°，
∵BC的中垂线交BC于点E，
∴BF=CF，
∴∠FCB=24°，
∴∠ACF=72°-24°=48°，
故选：A．
点评 此题主要考查了线段垂直平分线的性质，以及三角形内角和定理，关键是掌握线段垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
名校课堂系列答案
相关题目
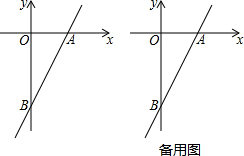
如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点，则∠OAB的大小的变化趋势为（ ）
如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标分别为A（-2，1）和B（-2，-3），那么第一架轰炸机C的平面坐标是（2，-1）．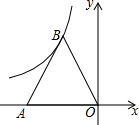
如图，等边三角形AOB的顶点A的坐标为（-4，0），顶点B在反比例函数y=$\frac{k}{x}$（x＜0）的图象上，则k=-4$\sqrt{3}$．