题目内容
10.先化简,再求值:$\frac{2{x}^{2}+{y}^{2}}{x+y}-\frac{{x}^{2}+2{y}^{2}}{x+y}$,已知x=tan60°,y=cos30°.分析 先根据分式混合运算的法则把原式进行化简,再求出x、y的值代入进行计算即可.
解答 解:原式=$\frac{2{x}^{2}+{y}^{2}-{x}^{2}-2{y}^{2}}{x+y}$
=$\frac{{x}^{2}-{y}^{2}}{x+y}$
=x-y,
当x=tan60°=$\sqrt{3}$,y=cos30°=$\frac{\sqrt{3}}{2}$时,原式=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
20.甲乙两种水稻试验品中连续5年的平均单位面积产量如下(单位:吨/公顷)
(1)甲乙两种水稻试验品的中位数分别是多少?
(2)甲乙两种水稻试验品的平均数分别是多少?
(3)试根据这组数据估计哪中水稻品种的产量比较稳定.
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
(2)甲乙两种水稻试验品的平均数分别是多少?
(3)试根据这组数据估计哪中水稻品种的产量比较稳定.
1.下列各数中,绝对值最大的实数是( )
| A. | π | B. | -2 | C. | $\frac{4}{3}$ | D. | -$\sqrt{7}$ |
18. 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
 如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )
如图,DE∥GF,A在DE上,C在GF上△ABC为等边三角形,其中∠EAC=80°,则∠BCG度数为( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
15.下列各组数中,运算结果为负数的是( )
| A. | 2-3 | B. | (-2)-3 | C. | 3-2 | D. | (-3)2 |
19.计算3x4÷x2=( )
| A. | 3x2 | B. | 2x2 | C. | x2 | D. | 3x6 |
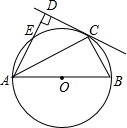 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.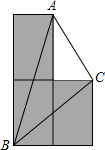 用3块形状、大小先完全相同的长方形小木片,拼成知图所示的“L”形,点A,B,C分别是其中的3个顶点,若AB=8cm,CB=6cm,则AC=2$\sqrt{5}$cm.
用3块形状、大小先完全相同的长方形小木片,拼成知图所示的“L”形,点A,B,C分别是其中的3个顶点,若AB=8cm,CB=6cm,则AC=2$\sqrt{5}$cm.