题目内容
16.先化简,再求值:$\frac{3x-9}{{x}^{2}-1}$÷$\frac{x-3}{{x}^{2}+2x+1}$-(3-$\frac{3}{1-x}$),其中x=$\sqrt{3}$+1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{3(x-3)}{(x+1)(x-1)}$•$\frac{(x+1)^{2}}{x-3}$-$\frac{3(x-1)+3}{x-1}$
=$\frac{3(x+1)}{x-1}$-$\frac{3x}{x-1}$
=$\frac{3}{x-1}$,
故当x=$\sqrt{3}$+1时,原式=$\frac{3}{\sqrt{3}+1-1}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
7.下列运算正确的是( )
| A. | 3a2-a2=3 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | a6÷a3=a2 |
11.下列运算正确的是( )
| A. | a3+a4=a7 | B. | a8÷a2=a4 | C. | (2a4)3=8a7 | D. | 2a3•a4=2a7 |

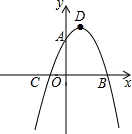 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.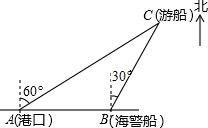 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).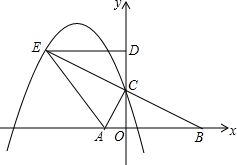 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.