题目内容
11. 如图,AD∥BC,AB=AD=DC,∠ABC=∠DCB,点E、F分别为DC、BC上一动点,且满足∠EAF=$\frac{1}{2}$∠BAD,EG∥BC交AF于G.探究线段DE、BF和GE的数量关系.
如图,AD∥BC,AB=AD=DC,∠ABC=∠DCB,点E、F分别为DC、BC上一动点,且满足∠EAF=$\frac{1}{2}$∠BAD,EG∥BC交AF于G.探究线段DE、BF和GE的数量关系.
分析 延长CB,截取BM=DE,连接AM、EF,由平行线的性质和已知条件得出∠D=∠ABM,由SAS证明△ABM≌△ADE,得出∠BAM=∠DAE,AM=AE,证出∠MAF=∠EAF,由SAS证明△AEF≌△AMF,得出EF=MF=DE+BF,∠AFE=∠AFM,由平行线的性质证出∠EFA=∠EGF,得出EG=EF,即可得出结论.
解答 解:DE+BF=GE;理由如下: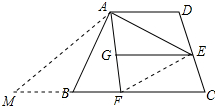
延长CB,截取BM=DE,连接AM、EF,如图所示:
∵AD∥BC,
∴∠DCB+∠D=180°,
∵∠ABC=∠DCB,
∴∠ABC+∠D=180°,
∵∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABM=∠D}&{\;}\\{BM=DE}&{\;}\end{array}\right.$,
∴△ABM≌△ADE(SAS),
∴∠BAM=∠DAE,AM=AE,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠DAE+∠BAF=∠EAF,
∴∠BAF+∠BAM=∠EAF,
∴∠MAF=∠EAF,
在△AEF和△AMF中,$\left\{\begin{array}{l}{AE=AM}&{\;}\\{∠EAF=∠MAF}&{\;}\\{AF=AF}&{\;}\end{array}\right.$,
∴△AEF≌△AMF(SAS),
∴EF=MF=DE+BF,∠AFE=∠AFM,
∵EG∥BC,
∴∠EGF=∠AFM,
∴∠EFA=∠EGF,
∴GE=EF,
∴DE+BF=GE.
点评 本题考查了全等三角形的判定与性质、梯形的性质、等腰三角形的判定与性质等知识;本题综合性强,有一定难度,需要通过作辅助线两次证明三角形全等才能得出结论.

 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | x |
| B | 75~89 | 20 | 0.4 |
| C | 60~74 | n | 0.16 |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
 如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.
如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.
 已知:如图,△ABC、△CDE、△EHK都是等边三角形,且A、D、K共线,AD=DK,求证:△HBD也是等边三角形.
已知:如图,△ABC、△CDE、△EHK都是等边三角形,且A、D、K共线,AD=DK,求证:△HBD也是等边三角形.

 如图,长方形纸片ABCD中,AB=10cm,BC=8cm,E为BC上的一点,将纸片沿AE翻折,使点B与CD边上的点F重合.求线段EF的长.
如图,长方形纸片ABCD中,AB=10cm,BC=8cm,E为BC上的一点,将纸片沿AE翻折,使点B与CD边上的点F重合.求线段EF的长.