题目内容
5. 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E,连结DE,下列五个结论:
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,交AC边于点E,连结DE,下列五个结论:①BD=DE;②△CDE是等腰三角形;③2DE2=CA•CE;④DE=AB•sinB;⑤$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=cos2C.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 连接AD,根据圆周角定理得出AD⊥BC,BE⊥AC,根据等腰三角形三线合一的性质得出CD=BD,然后根据直角三角形斜边中线的性质得出DE=DC=BD,即可判断①②正确;证得△DCE∽△ABC,根据相似三角形的性质得出$\frac{CE}{BC}$=$\frac{DE}{CA}$,进一步得出2DE2=CA•CE,即可判断③正确;通过解直角三角形即可判断④错误;根据相似三角形的性质得出$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=($\frac{EC}{BC}$)2,又因为在RT△BEC中,sinC=$\frac{EC}{BC}$,即可判断⑤正确.
解答 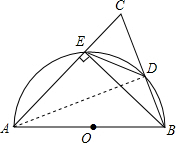 解:连接AD,
解:连接AD,
∵AB为直径,
∴AD⊥BC,BE⊥AC,
∵AB=AC,
∴DC=BD,
∴DE=DC=BD,故①②正确;
∵∠CED=∠ABD=∠ACD,
∴△DCE∽△ABC,
∴$\frac{CE}{BC}$=$\frac{DE}{CA}$,
∵BC=2DE,
∴2DE2=CA•CE,故③正确;
∵sinB=$\frac{AD}{AB}$,
∴AD=AB•sinB,
∵AD≠DE,
∴DE≠AB•sinB,故④错误;
∵△DCE∽△ABC,
∴$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=($\frac{EC}{BC}$)2,
∵AB为直径,
∴∠CEB=90°,
∴sinC=$\frac{EC}{BC}$,
∴$\frac{{S}_{△DEC}}{{S}_{△ABC}}$=cos2C,故⑤正确;
所以正确的结论有①②③⑤4个,
故选D.
点评 本题考查了圆周角定理,直角三角函数,三角形相似的判定和性质,直角三角形斜边中线的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
16. 如图,点A在双曲线y=$\frac{k}{x}$上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC-AC=2,则k的值为( )
如图,点A在双曲线y=$\frac{k}{x}$上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC-AC=2,则k的值为( )
 如图,点A在双曲线y=$\frac{k}{x}$上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC-AC=2,则k的值为( )
如图,点A在双曲线y=$\frac{k}{x}$上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC-AC=2,则k的值为( )| A. | 8-2$\sqrt{7}$ | B. | 8+2$\sqrt{7}$ | C. | 3 | D. | 6 |
 如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12.
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为4,△EBA的周长为12. 已知:如图,Rt△ABC中,AC=2BC,∠ABC=90°,将Rt△ABC绕点C按顺时针方向旋转,使顶点B落在AC上的点E处,得到△DEC,再将Rt△ABC沿着AB所在直线翻折(离开原所在平面)180°后.得到△ABF,连接DA.
已知:如图,Rt△ABC中,AC=2BC,∠ABC=90°,将Rt△ABC绕点C按顺时针方向旋转,使顶点B落在AC上的点E处,得到△DEC,再将Rt△ABC沿着AB所在直线翻折(离开原所在平面)180°后.得到△ABF,连接DA.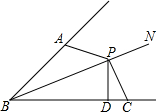 已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.