题目内容
 如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )
如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )A、2
| ||
B、3
| ||
C、4
| ||
| D、6 |
考点:菱形的性质
专题:
分析:由菱形ABCD中,对角线BD=3,∠BAD=60°,根据菱形的性质,可得OA=
=
,继而求得答案.
| OB |
| tan30° |
3
| ||
| 2 |
解答: 解:连接AC,交BD于点O,
解:连接AC,交BD于点O,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=
BD=
,∠BAO=
∠BAD=
×60°=30°,
∴OA=
=
,
∴AC=2OA=3
.
故选B.
 解:连接AC,交BD于点O,
解:连接AC,交BD于点O,∵四边形ABCD是菱形,
∴AC⊥BD,OB=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=
| OB |
| tan30° |
3
| ||
| 2 |
∴AC=2OA=3
| 3 |
故选B.
点评:此题考查了菱形的性质以及三角函数.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
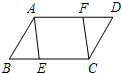 如图,?ABCD中,点E在BC上.若点F在AD上,则△CDF与△ABE不一定全等的条件是( )
如图,?ABCD中,点E在BC上.若点F在AD上,则△CDF与△ABE不一定全等的条件是( )| A、DF=BE |
| B、AF=CE |
| C、CF=AE |
| D、CF∥AE |
 如图,P是等边△ABC内的一点,且PA=4,PB=2
如图,P是等边△ABC内的一点,且PA=4,PB=2 如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.
如图是一个由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出它从正面和从左面看到的形状图.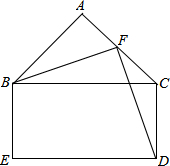 如图,在△ABC中,∠A=90°,AB=AC,F为AC边上中点,四边形BEDC是矩形,且BC=2BE,求证:△FBD是等腰三角形.
如图,在△ABC中,∠A=90°,AB=AC,F为AC边上中点,四边形BEDC是矩形,且BC=2BE,求证:△FBD是等腰三角形. 如图所示,AB是圆O的一条弦,OD⊥AB,垂足C,交圆O于D,E在圆O上.
如图所示,AB是圆O的一条弦,OD⊥AB,垂足C,交圆O于D,E在圆O上. 如图:已知a、b两数在数轴上的位置.
如图:已知a、b两数在数轴上的位置.