题目内容
15.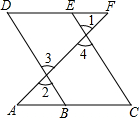 如图,E点为DF上的点,B为AC上的点,如果∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.
如图,E点为DF上的点,B为AC上的点,如果∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由.解:∵∠2=∠3,∠1=∠4(对顶角相等)
又∵∠1=∠2(已知)
∴∠3=∠4(等量代换)
∴BD∥CE(内错角相等,两直线平行)
∴∠C=∠ABD(两直线平行,同位角相等)
又∵∠C=∠D(已知)
∴∠ABD=∠D(等量代换)
∴DF∥AC(内错角相等,两直线平行)
分析 求出∠3=∠4,根据平行线的判定推出BD∥CE,根据平行线的性质得出∠C=∠ABD,求出∠ABD=∠D,根据平行线的判定推出即可.
解答 解:∵∠2=∠3,∠1=∠4(对顶角相等),
又∵∠1=∠2(已知)
∴∠3=∠4(等量代换),
∴BD∥CE(内错角相等,两直线平行),
∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D,
∴∠ABD=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
故答案为:对顶角相等,等量代换,BD,CE,内错角相等,两直线平行,两直线平行,同位角相等,∠ABD,∠D,等量代换,内错角相等,两直线平行.
点评 本题考查了平行线的性质和判定的应用,能运用性质和判定定理进行推理是解此题的关键,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若式子$\sqrt{2x-1}$+$\root{3}{1-x}$有意义,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤1 | C. | $\frac{1}{2}$≤x≤1 | D. | 以上答案都不对 |
10.在同一平面内,已知a⊥b,b⊥c,则直线a与直线c的关系为( )
| A. | 平行 | B. | 垂直 | C. | 相交 | D. | 不平行 |
7.在同一个平面内,直线a、b相交于点P,a∥c,b与c的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 重合 | D. | 平行或相交 |
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.