题目内容
7.“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图尚不完整的扇形统计图和条形统计图,请你根据统计图中所提供的信息解答下列问题:(1)请补全条形统计图;
(2)若该中学共有学生1200人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
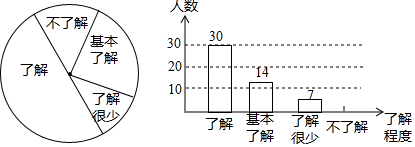
分析 (1)根据了解的人数和所占的百分百求出抽查的总人数,用总人数减去了解、基本了解和了解很少的人数,求出不了解的人数,从而补全统计图;
(2)用该中学的总人数乘以“了解”和“基本了解”所占的百分比即可;
(3)根据题意先画出树状图,再根据概率公式即可得出答案.
解答 解:(1)根据题意得:
30÷50%=60(人),
则不了解的人数是:60-30-14-7=9(人);
补图如下:
(2)根据题意得:1200×$\frac{30+14}{60}$=880(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为880人;
(3)画树状图得:
∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为:$\frac{12}{20}$=$\frac{3}{5}$.
点评 此题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,读懂题意,根据题意求出总人数是解题的关键;概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 在四边形ABCD中,AB=3,BC=4,AD=5$\sqrt{2}$,CD=5,∠ABC=90°,求对角线BD的长.
在四边形ABCD中,AB=3,BC=4,AD=5$\sqrt{2}$,CD=5,∠ABC=90°,求对角线BD的长. 如图,Rt△ABC中,∠BCA=90°,AB=$\sqrt{5}$,AC=2,D为斜边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,连接EF,则EF的最小值是$\frac{2\sqrt{5}}{5}$.
如图,Rt△ABC中,∠BCA=90°,AB=$\sqrt{5}$,AC=2,D为斜边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为E、F,连接EF,则EF的最小值是$\frac{2\sqrt{5}}{5}$.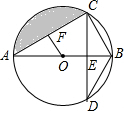 如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F.
如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F.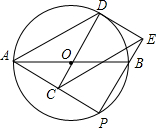 如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
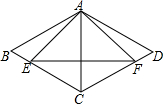 如图,在菱形ABCD中,E、F分别为边BC、CD上一点且BE=DF.
如图,在菱形ABCD中,E、F分别为边BC、CD上一点且BE=DF.