题目内容
12．约分：（1）$\frac{{x}^{2}+4x+4}{{x}^{2}-4}$．
（2）$\frac{m-2}{m（2-m）^{2}}$．
（3）$\frac{{x}^{2}-4}{（x-2）^{2}}$．
分析 （1）先将分子、分母分别进行因式分解，再约去它们的公因式即可；
（2）先将（2-m）2变形为（m-2）2，再约去分子与分母的公因式即可；
（3）先将分子进行因式分解，再约去分子与分母的公因式即可．
解答 解：（1）$\frac{{x}^{2}+4x+4}{{x}^{2}-4}$=$\frac{（x+2）^{2}}{（x+2）（x-2）}$=$\frac{x+2}{x-2}$；
（2）$\frac{m-2}{m（2-m）^{2}}$=$\frac{m-2}{m（m-2）^{2}}$=$\frac{1}{m（m-2）}$；
（3）$\frac{{x}^{2}-4}{（x-2）^{2}}$=$\frac{（x+2）（x-2）}{（x-2）^{2}}$=$\frac{x+2}{x-2}$．
点评 本题考查了约分的定义以及方法．约去分式的分子与分母的公因式，不改变分式的值，这样的分式变形叫做分式的约分．由约分的概念可知，要首先将分子、分母转化为乘积的形式，再找出分子、分母的最大公因式并约去，注意不要忽视数字系数的约分．
练习册系列答案
通城学典默写能手系列答案
相关题目
17．为了准备小颖六年后上大学的学费15000元，她的父亲现在就参加了教育储蓄．下面有两种蓄方式：
（1）先存一个三年期的，三年后将本息和自动转存一个三年期；
（2）直接存一个六年期的．
你认为哪种储蓄方式开始存入的本金比较少？
（1）先存一个三年期的，三年后将本息和自动转存一个三年期；
（2）直接存一个六年期的．
你认为哪种储蓄方式开始存入的本金比较少？
| 期数 | 教育储蓄年利率/% |
| 一年 | 2.25 |
| 三年 | 3.24 |
| 六年 | 3.60 |
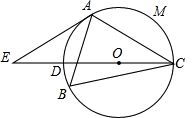已知：△ABC内接于⊙O，∠B=60°，点E是直径CD的延长线上的一点，且AE=AC．