题目内容
1.若y=$\frac{2x-3}{{x}^{2}+1}$,当x为何值时.(1)y值为0?
(2)y值为正数?
(3)y值为负数?
分析 (1)根据分子为零,可得函数值为零;
(2)根据分子为大于零,可得函数值大于零;
(3)根据分子小于零,可得函数小于零.
解答 解:(1)由y=$\frac{2x-3}{{x}^{2}+1}$=0,得2x-3=0,
解得x=$\frac{3}{2}$,
当x=$\frac{3}{2}$时,y值为零;
(2)由y=$\frac{2x-3}{{x}^{2}+1}$>0,得2x-3>0,
解得x>$\frac{3}{2}$,
当时x$>\frac{3}{2}$,y值为正数;
(3)由y=$\frac{2x-3}{{x}^{2}+1}$<0,得2x-3<0,
解得x<$\frac{3}{2}$,
当时x<$\frac{3}{2}$,y值为负数.
点评 本题考查了函数值,利用函数与方程的关系,函数与不等式的关系.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.下列运算正确的是( )
| A. | 2-3=-6 | B. | (-2)3=-6 | C. | ($\frac{2}{3}$)-2=$\frac{4}{9}$ | D. | 2-3=$\frac{1}{8}$ |
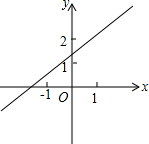 直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.
直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.