题目内容
4.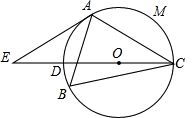 已知:△ABC内接于⊙O,∠B=60°,点E是直径CD的延长线上的一点,且AE=AC.
已知:△ABC内接于⊙O,∠B=60°,点E是直径CD的延长线上的一点,且AE=AC.(1)求证:AE是⊙O的切线.
(2)若DE=1,用扇形OAMC围成一个圆锥的侧面,求该圆锥的表面积.
分析 (1)利用圆周角定理以及等腰三角形的性质得出∠E=∠ACE=∠OCA=∠OAC=30°,∠EAC=120°,进而得出∠EAO=90°,即可得出答案;
(2)首先求出AD=ED=1,进而求得圆的半径为1,求得扇形的面积和弧长,根据弧长求得圆锥的底面积,然后即可求得圆锥的表面积.
解答 (1)证明:连接AO,
∵∠B=60°,
∴∠AOC=120°,
∵AO=CO,AE=AC,
∴∠E=∠ACE,∠OCA=∠OAC=30°,
∴∠E=∠ACE=∠OCA=∠OAC=30°,
∴∠EAC=120°,
∴∠EAO=90°,
∴AE是⊙O的切线;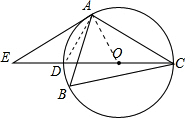
(2)解:连接AD,
∵DC是⊙O的直径,
∴∠DAC=90°,
∵∠ADC=∠B=60°,∠E=30°,
∴∠EAD=30°,
∴∠E=∠EAD,
∴AD=ED=1,
∵∠ACD=30°,
∴DC=2AD=2,
∴OC=1,
∴S扇形OAMC=$\frac{120π×{1}^{2}}{360}$=$\frac{1}{3}$π,
弧AC的长:$\frac{120π×1}{180}$=$\frac{2}{3}$π,
圆锥底的面积:π($\frac{\frac{2}{3}π}{2π}$)2=$\frac{1}{9}$π,
∴该圆锥的表面积:$\frac{1}{3}$π+$\frac{1}{9}$π=$\frac{4}{9}$π.
点评 此题主要考查了圆周角定理以及切线的判定、等腰三角形的性质等知识,作出辅助线构建直角三角形和等腰三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
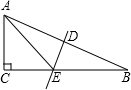 在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.
在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.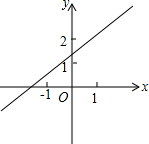 直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.
直线l:y=(m-3)x+n(m,n为常数)如图所示,化简|m-n+3|+$\sqrt{{n}^{2}-4n+4}$-|m-1|.