题目内容
6.为了抓住保国寺建寺1000年的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
分析 (1)关系式为:A种纪念品8件需要钱数+B种纪念品3件钱数=950;A种纪念品5件需要钱数+B种纪念品6件需要钱数=800;
(2)关系式为:用于购买这100件纪念品的资金不少于7500元,但不超过7650元,得出不等式组求出即可.
解答 解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,
根据题意得方程组得:$\left\{\begin{array}{l}{8a+3b=950}\\{5a+6b=800}\end{array}\right.$,
解方程组得:$\left\{\begin{array}{l}{a=100}\\{b=50}\end{array}\right.$,
∴购进一件A种纪念品需要100元,购进一件B种纪念品需要50元;
(2)设该商店购进A种纪念品x个,则购进B种纪念品有(100-x)个,
∴$\left\{\begin{array}{l}{100x+50(100-x)≥7500}\\{100x+50(100-x)≤7650}\end{array}\right.$,
解得:50≤x≤53,
∵x 为正整数,x=50,51,52,53
∴共有4种进货方案,
分别为:方案1:商店购进A种纪念品50个,则购进B种纪念品有50个;
方案2:商店购进A种纪念品51个,则购进B种纪念品有49个;
方案3:商店购进A种纪念品52个,则购进B种纪念品有48个;
方案4:商店购进A种纪念品53个,则购进B种纪念品有47个.
点评 此题主要考查了二元一次方程组的应用以及一元一次方程的应用,找到相应的关系式是解决问题的关键,注意第二问应求得整数解.

练习册系列答案
相关题目
1.为了参加市中学生篮球运动会,一支校篮球队准备购买10双运动鞋,各种尺码的统计如下表所示,则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码/厘米 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量/双 | 2 | 4 | 2 | 1 | 1 |
| A. | 25.5,26 | B. | 26,25.5 | C. | 26,26 | D. | 25.5,25.5 |
18.在0,2,-3,-$\frac{2}{3}$这四个数中,最大的数是( )
| A. | 0 | B. | 2 | C. | -3 | D. | -$\frac{2}{3}$ |
15.分解因式:y3-4y2+4y=( )
| A. | y(y2-4y+4) | B. | y(y-2)2 | C. | y(y+2)2 | D. | y(y+2)(y-2) |

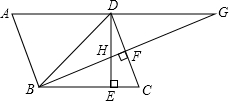 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中: