题目内容
10.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长BC与宽AB的关系是( )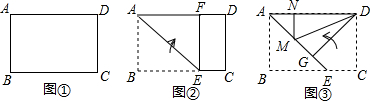
| A. | BC=2AB | B. | BC=$\sqrt{3}$AB | C. | BC=1.5AB | D. | BC=$\sqrt{2}$AB |
分析 连接DE,由翻折的性质知,四边形ABEF为正方形,∠EAD=45°,而M点正好在∠NDG的平分线上,则DE平分∠GDC,由折叠性质得出Rt△DGE≌Rt△DCE,得到DC=DG,而△AGD为等腰直角三角形,得到AD=$\sqrt{2}$DG=$\sqrt{2}$CD,因此BC=$\sqrt{2}$AB.
解答 解:连接DE,如图,
∵沿过A点的直线折叠,使得B点落在AD边上的点F处,
∴四边形ABEF为正方形,
∴∠EAD=45°,
由第二次折叠知,M点正好在∠NDG的平分线上,
∴DE平分∠GDC,Rt△DGE≌Rt△DCE,
∴DC=DG,
又∵△AGD为等腰直角三角形,
∴AD=$\sqrt{2}$DG=$\sqrt{2}$CD,
∴BC=$\sqrt{2}$AB.
故选:D.
点评 本题考查了翻折的性质:翻折前后的两个图形全等.也考查了正方形、角的平分线的性质以及等腰直角三角形的性质;熟记翻折变换和正方形的性质是解决问题的关键.

练习册系列答案
相关题目
2.小明在下面的计算中只做对了一道题,他做对的题目是( )
| A. | ($\frac{a}{b}$)2=$\frac{{a}^{2}}{b}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{x}^{2}-{y}^{2}}{x-y}=x+y$ | D. | $\frac{-x-y}{x-y}=-1$ |
 C. 2 D.
C. 2 D. 
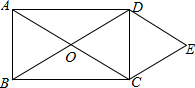 如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.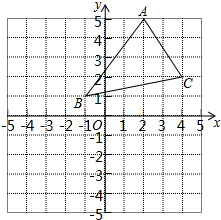 如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.
如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.