题目内容
2.绝对值大于2而小于6的所有整数的和是多少?(列式计算)分析 根据题意画出图形,由绝对值的几何意义可知:绝对值大于2小于6的所有整数即为到原点的距离大于2小于6,观察数轴即可得到满足题意的所有整数,求出这些整数之和即可.
解答 解:根据题意画出数轴,如图所示:
根据图形得:绝对值大于2而小于6的所有整数有:-3,-4,-5,3,4,5,
这几个整数的和为:
(-3)+(-4)+(-5)+3+4+5
=[(-3)+3]+[(-4)+4]+[(-5)+5]
=0.
答:绝对值大于2而小于6的所有整数的和是0.
点评 此题考查了绝对值的几何意义,即一个数的绝对值就是在数轴上表示这个数的点到原点的距离,离原点越近,绝对值越小;离原点越远,绝对值越大.另外在求和时利用加法的运算律可以简化运算,同时注意数形结合思想的灵活运用.

练习册系列答案
相关题目
8. 如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
 如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
17.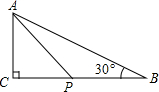 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
 如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
如图,△ABC中,∠C=90°,AC=2.5,∠B=30°,点P是BC边上的动点,则AP长不可能是( )| A. | 3 | B. | 3.5 | C. | 4.8 | D. | 5.2 |
14.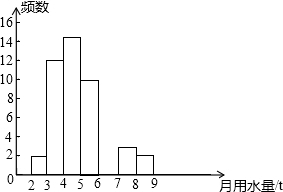 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
(1)频数分布表中a=15,b=30%.(填百分比),c=6;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有279户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | a | b |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | c | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有279户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
11. 如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
 如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )| A. | 5$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
12.若二次函数y=x2-6x+9的图象经过A(-1,y1),B(1,y2),C(3+$\sqrt{3}$,y3)三点.则关于y1,y2,y3大小关系正确的是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y3>y1>y2 |
 如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,则∠BCD的度数为100°.
如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,则∠BCD的度数为100°.