题目内容
7. 如图,四边形ABCD是正方形,射线BE∥AC,点F是BE上的任意一点,CE∥AF.
如图,四边形ABCD是正方形,射线BE∥AC,点F是BE上的任意一点,CE∥AF.求证:四边形AFEC的面积等于正方形ABCD的面积.
分析 过点C作CG∥AB,因为BE∥AC,CG∥AB,所以四边形CABG是平行四边形,CG=AB,同理:四边形AFEC是平行四边形,CE=AF 可证明:△ABF≌△CGE(SSS)所以,四边形AFEC面积=四边形CABG面积而正方形ABCD的面积=四边形CABG面积(同底等高)四边形AFEC的面积等于正方形ABCD的面积.
解答 证明:过点C作CG∥AB,
∵BE∥AC,CG∥AB,
∴四边形CABG是平行四边形,
∴CG=AB,
同理可证:四边形AFEC是平行四边形,
∴CE=AF,
∵GE=AC-FG,BF=AC-FG,
∴BF=FG,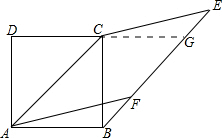
在△ABF和△CGE中
$\left\{\begin{array}{l}{AF=CE}\\{AB=CG}\\{BF=GE}\end{array}\right.$,
∴△ABF≌△CGE(SSS),
∴四边形AFEC面积=四边形CABG面积,
又∵正方形ABCD的面积=四边形CABG面积(同底等高),
四边形AFEC的面积等于正方形ABCD的面积.
点评 本题考查了正方形的性质、全等三角形的判定和性质以及平行四边形的判定和性质,解题的关键是正确添加辅助线构造全等三角形,得到四边形AFEC面积=四边形CABG面积.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,∠1=∠2,∠3=∠4,且AD⊥DC,AE⊥BE,求证:DE∥BC.
如图,∠1=∠2,∠3=∠4,且AD⊥DC,AE⊥BE,求证:DE∥BC. 如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.
如图,已知△ABC中,∠C=90°,D为BC边上任意一点,试问点D在BC上运动的过程中,AB2-AD2与BC2-CD2的大小关系是怎样?证明你的结论.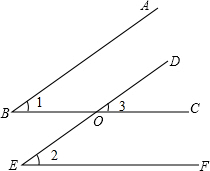 如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF.
如图所示,有3个论断:①AB∥DE;②∠1=∠2;③BC∥EF.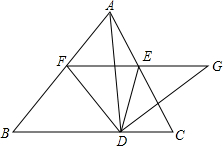 如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.
如图,△ABC中,AD⊥BC于D,点E在AC上,EF∥BC交AB于F,且DF平分∠BDE,DG⊥DF交FE的延长线于G.