题目内容
11.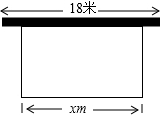 学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成.
学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成.(1)设围成的矩形平行墙的一边为x,请用含x的代数式来表示所囤成矩形的面积S,求出x的取值范围;
(2)当矩形自行车棚的长为何值时,面积S有最大值;
(3)矩形自行车棚的面积S=50平方米,则请求出此时矩形自行车棚的长和宽.
分析 (1)因为平行墙的一边为x,所以垂直于墙的一边为($\frac{25-x}{2}$)米,由长方形的面积列式即可;
(2)车棚的面积为50平方米,即S=50,建立方程,求得结论.
解答 解:(1)S=x($\frac{25-x}{2}$)=-$\frac{1}{2}$x2+$\frac{25}{2}$x(0<x<18);
(2)∵S=-$\frac{1}{2}$x2+$\frac{25}{2}$x,
∴当x=$\frac{25}{2}$时,面积S有最大值;
(3)依题意得,-$\frac{1}{2}$x2+$\frac{25}{2}$x=50,
解得:x1=20(不合题意舍去),x2=5,
∴$\frac{25-5}{2}$=10,
∴矩形自行车棚的长为10米,宽为5米.
点评 主要考查了二次函数的应用,一元二次方程的应用;得到垂直于墙的一边的关系式是解决本题的易错点.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.
如图所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若∠AOC=36°,则∠EOF=54°.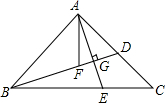 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由. 已知,如图,AD=BC,AB=CD.
已知,如图,AD=BC,AB=CD.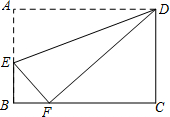 如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )
如图,长方形ABCD中,点E 在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处,若AD=5,DC=3,则BF的长是( )