题目内容
7.△ABC三边a,b,c满足a2+b2+c2=ab+bc+ca,则△ABC的形状是等边三角形.分析 分析题目所给的式子,将等号两边均乘以2,再化简得(a-b)2+(a-c)2+(b-c)2=0,得出:a=b=c,即选出答案.
解答 解:等式a2+b2+c2=ab+bc+ac等号两边均乘以2得:
2a2+2b2+2c2=2ab+2bc+2ac,
即a2-2ab+b2+a2-2ac+c2+b2-2bc+c2=0,
即(a-b)2+(a-c)2+(b-c)2=0,
解得:a=b=c,
所以,△ABC是等边三角形.
故答案为:等边三角形.
点评 此题考查了因式分解的应用;利用等边三角形的判定,化简式子得a=b=c,由三边相等判定△ABC是等边三角形.

练习册系列答案
相关题目
15.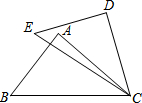 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )| A. | AB=DE,∠B=∠E | B. | AB=DE,AC=DC | C. | BC=EC,∠BCE=∠ACD | D. | BC=EC,AC=DC |
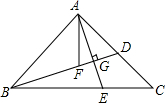 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.