题目内容
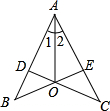 如图,CD⊥AB,BE⊥AC,垂足为D、E,BE、CD相交于O点,∠1=∠2,AB=AC,图中全等的三角形共有( )
如图,CD⊥AB,BE⊥AC,垂足为D、E,BE、CD相交于O点,∠1=∠2,AB=AC,图中全等的三角形共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
考点:全等三角形的判定
专题:
分析:在△ADO和△AEO中可利用AAS判定全等,可得到AD=AE,结合条件可得∠B=∠C,从而可证明△BOD和△COE全等,在△ABO和△ACO中利用SAS可证明全等,可得出答案.
解答:解:
在△ABO和△ACO中
∴△ABO≌△ACO(SAS),
∴∠D=∠C,BO=CO,
在△ADO和△AEO中
∴△ADO≌△ACO(AAS),
在△BOD和△COE中
∴△BOD≌△COE(ASA),
所以全等的三角形有三对,
故选C.
在△ABO和△ACO中
|
∴△ABO≌△ACO(SAS),
∴∠D=∠C,BO=CO,
在△ADO和△AEO中
|
∴△ADO≌△ACO(AAS),
在△BOD和△COE中
|
∴△BOD≌△COE(ASA),
所以全等的三角形有三对,
故选C.
点评:本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法,即SSS、SAS、ASA、AAS和HL是解题的关键

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
下列各数:
,0,4.2121121112,
,2.369,-5;其中无理数的个数有( )
| π |
| 3 |
| 23 |
| 7 |
| A、4个 | B、3个 | C、2个 | D、1个 |
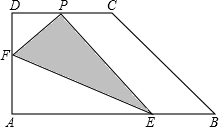 如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于
如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.当P落在直角梯形ABCD内部时,PD的最小值等于