题目内容
8.化简:$\frac{a\sqrt{b}+b\sqrt{a}}{a+\sqrt{b}}$•($\frac{\sqrt{b}}{\sqrt{ab}-b}$-$\frac{1}{\sqrt{a}+\sqrt{b}}$)÷$\frac{\sqrt{b}}{a-b}$.分析 根据二次根式的乘法法则和除法法则求解.
解答 解:原式=$\frac{a\sqrt{b}+b\sqrt{a}}{a+\sqrt{b}}$•($\frac{1}{\sqrt{a}-\sqrt{b}}$-$\frac{1}{\sqrt{a}+\sqrt{b}}$)÷$\frac{\sqrt{b}}{a-b}$
=$\frac{a\sqrt{b}+b\sqrt{a}}{a+\sqrt{b}}$•$\frac{2\sqrt{b}}{a-b}$•$\frac{a-b}{\sqrt{b}}$
=$\frac{2(a\sqrt{b}+b\sqrt{a})}{a+\sqrt{b}}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的乘法运算和除法运算法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.$\root{3}{-8}$等于( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | -$\frac{1}{2}$ | D. | -2 |
3.从正方形的四个顶点中,任取三个顶点连成三角形,对于事件M:“这个三角形是等腰三角形”.下列说法正确的是( )
| A. | 事件M为不可能事件 | B. | 事件M为必然事件 | ||
| C. | 事件M发生的概率为$\frac{1}{4}$ | D. | 事件M发生的概率为$\frac{1}{2}$ |
 如图,△ABC按顺时针方向旋转36°得到△EDC,且点D在A上,如果AB=AC,
如图,△ABC按顺时针方向旋转36°得到△EDC,且点D在A上,如果AB=AC,
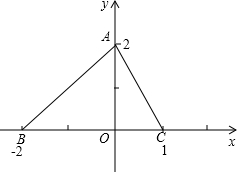 已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法.
已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法.