题目内容
6.解方程:(1)$\left\{\begin{array}{l}{x+2y=-3}\\{5x-3(x+y)=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{3(x-y-1)=y-9}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$.
分析 (1)方程组整理后,利用代入消元法求出解即可.
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)整理得$\left\{\begin{array}{l}{x+2y=-3}&{①}\\{2x-3y=1}&{②}\end{array}\right.$
由①得x=-3-2y ③
③代入②得2(-3-2y)-3y=1
-6-4y-3y=1
y=-1
y=-1代入③得x=-1
∴$\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$
(2)整理得$\left\{\begin{array}{l}{3x-4y=-6}&{①}\\{3x+2y=12}&{②}\end{array}\right.$
①-②得到-6y=-18
y=3
y=3代入①得到x=2
∴$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$
点评 本题考查的是二元一次方程的解法,解二元一次方程可用加减消元法和代入法,要根据方程的特点选择解法.

练习册系列答案
相关题目
17.通过估算比较大小,下列结论不正确的是( )
| A. | $\root{3}{69}$$>\sqrt{16}$ | B. | -$\sqrt{10}$>$\root{3}{-27}$ | C. | $\frac{\sqrt{7}-2}{2}<\frac{1}{2}$ | D. | $\sqrt{15}<2\sqrt{5}$ |
 如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是7和11.
如图是一个正方体纸盒的展开图,当折成纸盒时,与点1重合的点是7和11.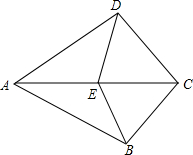 已知:∠ABC=∠ADC=90°,E是AC中点.
已知:∠ABC=∠ADC=90°,E是AC中点.