题目内容
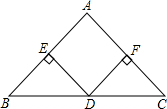 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.
如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.(1)添加的条件为 ①
(2)证明:
考点:正方形的判定
专题:开放型
分析:(1)根据正方形的判定方法可添加条件;
(2)连结AD.先由等腰三角形三线合一的性质得出AD平分∠BAC,再根据角平分线的性质得出DE=DF.
如果添加的条件为 ①∠BAC=90°,首先根据三个角是直角的四边形是矩形得出四边形EDFA是矩形,又DE=DF,那么可证四边形EDFA是正方形;
如果添加的条件为②DF∥AB,先由平行线的性质及垂直的定义得出∠BAC=∠DFC=90°,再证明四边形EDFA是矩形,又DE=DF,那么可证四边形EDFA是正方形.
(2)连结AD.先由等腰三角形三线合一的性质得出AD平分∠BAC,再根据角平分线的性质得出DE=DF.
如果添加的条件为 ①∠BAC=90°,首先根据三个角是直角的四边形是矩形得出四边形EDFA是矩形,又DE=DF,那么可证四边形EDFA是正方形;
如果添加的条件为②DF∥AB,先由平行线的性质及垂直的定义得出∠BAC=∠DFC=90°,再证明四边形EDFA是矩形,又DE=DF,那么可证四边形EDFA是正方形.
解答:解:(1)添加的条件为 ①∠BAC=90°,②DF∥AB.(方法很多,如∠B=45°或BC=
AB或DE⊥DF或F为AC中点或DE∥AC等).
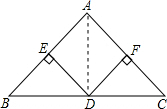 (2)连结AD.
(2)连结AD.
∵在△ABC中,AB=AC,D是BC的中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴DE=DF.
如果添加的条件为 ①∠BAC=90°,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴∠DEA=∠DFA=90°,
∵∠BAC=90°,
∴四边形EDFA是矩形,
又∵DE=DF,
∴四边形EDFA是正方形;
如果添加的条件为②DF∥AB,
∵DF∥AB,DF⊥AC于F,
∴∠BAC=∠DFC=90°,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴∠DEA=∠DFA=90°,
∴四边形EDFA是矩形,
又∵DE=DF,
∴四边形EDFA是正方形.
故答案为∠BAC=90°,DF∥AB.
| 2 |
 (2)连结AD.
(2)连结AD.∵在△ABC中,AB=AC,D是BC的中点,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴DE=DF.
如果添加的条件为 ①∠BAC=90°,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴∠DEA=∠DFA=90°,
∵∠BAC=90°,
∴四边形EDFA是矩形,
又∵DE=DF,
∴四边形EDFA是正方形;
如果添加的条件为②DF∥AB,
∵DF∥AB,DF⊥AC于F,
∴∠BAC=∠DFC=90°,
∵DE⊥AB,DF⊥AC,垂足分别为E、F,
∴∠DEA=∠DFA=90°,
∴四边形EDFA是矩形,
又∵DE=DF,
∴四边形EDFA是正方形.
故答案为∠BAC=90°,DF∥AB.
点评:本题主要考查了正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.

练习册系列答案
相关题目
设⊙O的半径为r,圆心O到直线l的距离为d,关于x的方程r2(x2+1)-2d2x=0有两个相等的实数根,则直线l与⊙O( )
| A、相离 | B、相切 |
| C、相交 | D、相切或相交 |
| 3 | 135 |
| 23 |
A、
| |||||
B、
| |||||
C、
| |||||
| D、无法确定 |
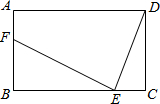 如图,在矩形ABCD中,AB=6,BC=9,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与线段AB交于点F,设CE=x.
如图,在矩形ABCD中,AB=6,BC=9,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与线段AB交于点F,设CE=x.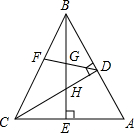 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2. 如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=
如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=