题目内容
当a，b为何值时，多项式ax2-x2-（b+2）xy+4x-3y+1没有x2和xy项．
考点：多项式
专题：
分析：根据合并同类项的法则，可合并同类项，再根据整式中不含有的项的系数是零，可得答案．
解答：解：合并同类项，得
ax2-x2-（b+2）xy+4x-3y+1=（a-1）x2-（b+2）xy+4x-3y+1，
由多项式中不含x2和xy项，得
a-1=0，b+2=0，
解得a=1，b=-2．
答：当a=1，b=-2时，多项式ax2-x2-（b+2）xy+4x-3y+1没有x2和xy项．
ax2-x2-（b+2）xy+4x-3y+1=（a-1）x2-（b+2）xy+4x-3y+1，
由多项式中不含x2和xy项，得
a-1=0，b+2=0，
解得a=1，b=-2．
答：当a=1，b=-2时，多项式ax2-x2-（b+2）xy+4x-3y+1没有x2和xy项．
点评：本题考查了多项式，在多项式中不含哪项，即哪项的系数为0，两项的系数互为相反数，合并同类项时为0．
练习册系列答案
相关题目
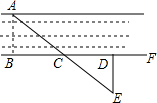如图，要测量河岸相对两点A，B的距离，可以从AB的垂线BF上取两点C，D．使BC=CD，过D作DE⊥BF，且A，C，E三点在一直线上，若测得DE=30米，即AB=
如图所示，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm．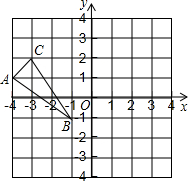
如图，△ABC三个顶点的坐标分别是A（-4，1），B（-1，-1），C（-3，2）．
如图，△ABC的三条高AD，BE，CF交于一点H，则点H是△DEF的（ ）| A、内心 | B、外心 | C、垂心 | D、重心 |
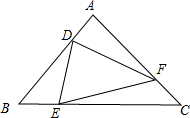等边△ABC边长为1，D、E、F分别在边AB、BC、CA上，△DEF也是等边三角形．
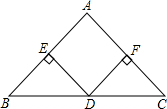如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F．只添加一个条件，使四边形EDFA是正方形．请你至少写出两种不同的添加方法．并选择一种证明．