题目内容
请构造图形设法求出15°,75°的三角函数值.
考点:解直角三角形
专题:计算题
分析:在△ABC中,∠C=90°,∠ABC=30°,AC=1,则BC=
AC=
,AB=2AC=2,延长CB到D,使BD=BA=2,连结AD,如图,易得∠D=15,再利用勾股定理计算出AD=
+
,然后根据锐角三角函数的定义计算15°,75°的三角函数值.
| 3 |
| 3 |
| 6 |
| 2 |
解答: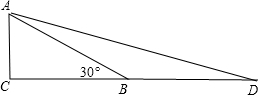 解:在△ABC中,∠C=90°,∠ABC=30°,AC=1,则BC=
解:在△ABC中,∠C=90°,∠ABC=30°,AC=1,则BC=
AC=
,AB=2AC=2,
延长CB到D,使BD=BA=2,连结AD,如图,
∵BA=BD,
∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,
∴∠D=15,
在Rt△ACD中,∵AC=1,BD=2+
,
∴AD=
=
=
•
=
•
=
+
,
∴sinD=sin15°=
=
,cosD=cos15°=
=
,tanD=tan15°=
=2-
,
∴sin75°=
,cos75°=
,tan75°=2+
.
 解:在△ABC中,∠C=90°,∠ABC=30°,AC=1,则BC=
解:在△ABC中,∠C=90°,∠ABC=30°,AC=1,则BC=| 3 |
| 3 |
延长CB到D,使BD=BA=2,连结AD,如图,
∵BA=BD,
∴∠D=∠BAD,
而∠ABC=∠D+∠BAD,
∴∠D=15,
在Rt△ACD中,∵AC=1,BD=2+
| 3 |
∴AD=
| AC2+DC2 |
8+4
|
| 2 |
4+2
|
| 2 |
(
|
| 6 |
| 2 |
∴sinD=sin15°=
| 1 | ||||
|
| ||||
| 4 |
2+
| ||||
|
| ||||
| 4 |
| 1 | ||
2+
|
| 3 |
∴sin75°=
| ||||
| 4 |
| ||||
| 4 |
| 3 |
点评:本题考查了解直角三角形在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
相关题目
 如图,△ABC的三条高AD,BE,CF交于一点H,则点H是△DEF的( )
如图,△ABC的三条高AD,BE,CF交于一点H,则点H是△DEF的( )| A、内心 | B、外心 | C、垂心 | D、重心 |
在直角坐标系中,O为坐标原点,已知点A(3,3),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
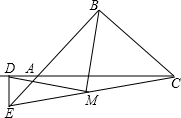 已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.
已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.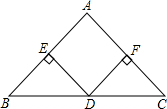 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.
如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.