题目内容
12. 如图,为了估计河的宽度,我们在河对岸选定了一个目标点O,在近岸取点A、C使O、A、C三点共线,且线段OC与河岸垂直,接着在过点C且与OC垂直的直线上选择适当的点D,使OD与近岸所在的直线交于点B.若测得AC=30m,CD=120cm,AB=40cm,求河的宽度OA.
如图,为了估计河的宽度,我们在河对岸选定了一个目标点O,在近岸取点A、C使O、A、C三点共线,且线段OC与河岸垂直,接着在过点C且与OC垂直的直线上选择适当的点D,使OD与近岸所在的直线交于点B.若测得AC=30m,CD=120cm,AB=40cm,求河的宽度OA.
分析 先证明△OAB∽△OCD,利用相似比得到$\frac{OA}{OA+30}$=$\frac{40}{120}$,然后根据比例的性质求OA.
解答 解:∵AB⊥OC,CD⊥OC,
∴AB∥CD,
∴△OAB∽△OCD,
∴$\frac{OA}{OC}$=$\frac{AB}{CD}$,即$\frac{OA}{OA+30}$=$\frac{40}{120}$,
∴OA=15.
故河的宽度OA为15cm.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.

练习册系列答案
相关题目
2.把多项式x2-3x+2分解因式,下列结果正确的是( )
| A. | (x-1)(x+2) | B. | (x-1)(x-2) | C. | (x+1)(x+2) | D. | (x+1)(x-2) |
17.下列函数中,是反比例函数的是( )
| A. | y=$\frac{k}{x}$ | B. | 3x+2y=0 | C. | xy-$\sqrt{2}$=0 | D. | y=$\frac{2}{x+1}$ |
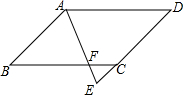 如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.
如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.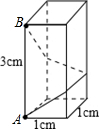 如图,长方体的底面是边长为1cm 的正方形,高为3cm.
如图,长方体的底面是边长为1cm 的正方形,高为3cm.