Question

19．边长为2的等边△ABC，用一个最小圆把它整个盖住，圆半径为$\frac{2\sqrt{3}}{3}$．

Answer 1

分析 作OD⊥BC于D，连接OB，由垂径定理得出BD=CD=$\frac{1}{2}$BC=1，由等边三角形的性质和已知条件得出∠OBD=$\frac{1}{2}$∠ABC=30°，由三角函数求出OB即可．

解答 解：作OD⊥BC于D，连接OB，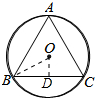
则BD=CD=$\frac{1}{2}$BC=1，
∵⊙O是等边三角形ABC的外接圆，
∴∠OBD=$\frac{1}{2}$∠ABC=30°，
∵cos∠OBD=$\frac{BD}{OB}$，
∴OB=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．

点评 本题考查的是等边三角形的性质、垂径定理、锐角三角函数的概念，熟练掌握等边三角形的性质，并能进行推理计算是解题的关键．