题目内容
14. 如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,DF=DC.
如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,DF=DC.求证:BF=AC.
分析 求出∠BDF=∠ADC=90°,∠FBD=∠CAD,根据AAS证出△BDF≌△ADC.
解答 证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠AEF=90°,
∵∠AFE+∠CAD+∠AEF=180°,∠FBD+∠BFD+∠BDA=180°,∠AFE=∠BFD,
∴∠FBD=∠CAD,
在△BDF和△ADC中
$\left\{\begin{array}{l}{∠FBD=∠CAD}\\{∠BDF=∠ADC=90°}\\{DF=DC}\end{array}\right.$,
∴△BDF≌△ADC(AAS),
∴BF=AC
点评 本题考查了全等三角形的性质和判定,垂直定义,三角形的内角和定理的应用,关键是推出△BDF≌△ADC.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
5.下列运算中没有意义的是( )
| A. | -2006÷[(-$\frac{7}{3}$)×3+7] | B. | [(-$\frac{7}{3}$)×3+7]÷(-2006) | C. | ($\frac{1}{3}$-$\frac{1}{2}$)÷[0-(-4)]×(-2) | D. | 2$\frac{1}{3}$÷(3$\frac{1}{3}$×6-18) |
 已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.
已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.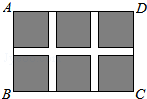 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?
如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?