题目内容
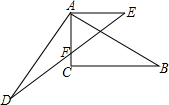 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.(1)求证:∠DAC=∠B;
(2)猜想线段AF、BC的关系.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由题意可以作辅助线即作DG⊥AC的延长线于G,然后根据平行线的性质可以推出结论;
(2)在第一问的基础上来由三角形的全等可以得到关系.
(2)在第一问的基础上来由三角形的全等可以得到关系.
解答: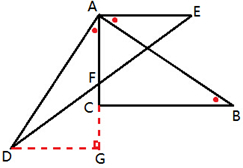 (1)证明:如图所示:作DG⊥AC的延长线于G
(1)证明:如图所示:作DG⊥AC的延长线于G
∵∠ACB=∠DAB=90°,AE∥BC,
∴∠CAE=180°-∠ACB=90°,∠B=∠BAE,
∴∠DAC=90°-∠BAC=∠BAE,
∴∠DAC=∠B;
(2)解:∵AG⊥DG,
∴∠AGD=∠ACB=90°,
在△ADG和△ABC中,
,
∴△ADG≌△ABC(AAS),
∴DG=AE;AG=BC,
在△AEF和△GDF中,
,
∴△AEF≌△GDF(AAS),
∴AF=GF=
AG=
BC,
∴BC=2AF.
 (1)证明:如图所示:作DG⊥AC的延长线于G
(1)证明:如图所示:作DG⊥AC的延长线于G∵∠ACB=∠DAB=90°,AE∥BC,
∴∠CAE=180°-∠ACB=90°,∠B=∠BAE,
∴∠DAC=90°-∠BAC=∠BAE,
∴∠DAC=∠B;
(2)解:∵AG⊥DG,
∴∠AGD=∠ACB=90°,
在△ADG和△ABC中,
|
∴△ADG≌△ABC(AAS),
∴DG=AE;AG=BC,
在△AEF和△GDF中,
|
∴△AEF≌△GDF(AAS),
∴AF=GF=
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=2AF.
点评:该题目考查了三角形的全等判定和性质、平行线的性质,关键是构造全等的三角形.

练习册系列答案
相关题目
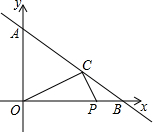 如图,直线y=-
如图,直线y=-| 3 |
| 4 |
| A、3≤m≤4 | ||
| B、2≤m≤4 | ||
C、0≤m≤
| ||
| D、0≤m≤3 |
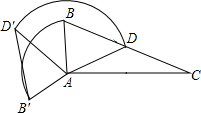 Rt△ABC中,∠BAC=90°,BC=6,点D为BC的中点,将△ABD绕点A按逆时针方向旋转120°得到△AB′D′,则点D在旋转过程中所经过的路程是多少?(结果保留π)
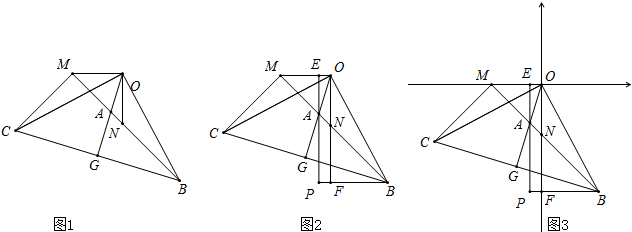
Rt△ABC中,∠BAC=90°,BC=6,点D为BC的中点,将△ABD绕点A按逆时针方向旋转120°得到△AB′D′,则点D在旋转过程中所经过的路程是多少?(结果保留π)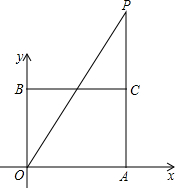 如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.
如图,长方形AOBC在直角坐标系中,A、B两点坐标分别为(8,0)、(0,6),点P是长方形一边所在直线上的一个动点,并且它位于y轴右侧.