题目内容
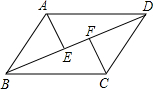 如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论.
如图,已知E、F在BD上,AE⊥BD于E,CF⊥BD于F,AD=BC,BE=DF,请问:△AED与△CFB全等吗?请说说明你的结论.考点:全等三角形的判定
专题:
分析:首先根据等式的性质可得BF=DE,再根据HL定理证明Rt△AED≌Rt△CBF.
解答:解:△AED与△CFB全等,理由如下:
∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
∵AE⊥BD于E,CF⊥BD于F,
∴∠AED=∠CFB=90°,
在Rt△AED和Rt△CBF中,
,
∴Rt△AED≌Rt△CBF(HL).
∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
∵AE⊥BD于E,CF⊥BD于F,
∴∠AED=∠CFB=90°,
在Rt△AED和Rt△CBF中,
|
∴Rt△AED≌Rt△CBF(HL).
点评:此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
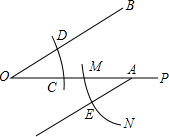 已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )
已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )| A、CD∥ME |
| B、OB∥AE |
| C、∠ODC=∠AEM |
| D、∠ACD=∠EAP |
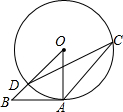 如图,AB与圆O相切于点A,且OA=AB,则∠DCA的度数是( )
如图,AB与圆O相切于点A,且OA=AB,则∠DCA的度数是( )| A、45° | B、30° |
| C、60° | D、22.5° |
 如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.
如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.A、
| ||
B、
| ||
| C、800π | ||
| D、500π |
 东山宾馆主楼梯准备铺上红地毯,已知这种地毯每平方米造价为25元,主楼梯宽2m,侧面如图所示,则购买这种地毯至少需要
东山宾馆主楼梯准备铺上红地毯,已知这种地毯每平方米造价为25元,主楼梯宽2m,侧面如图所示,则购买这种地毯至少需要 某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由.
某市有一座古塔,如图所示,底部是由多边形组成的,为了测量这座塔的塔底墙角(即∠ABC)的大小,请用所学知识设计方案,并说明理由. 如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?
如图,试探究∠EAB,∠B,∠BCD之间有怎样的关系时,才能使AE∥CD?