题目内容
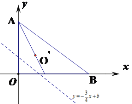
【题目】如图1,抛物线![]() 与x轴交于A,B两点
与x轴交于A,B两点![]() 在B的左侧
在B的左侧![]() ,与y轴交于C,且
,与y轴交于C,且![]() ,
,
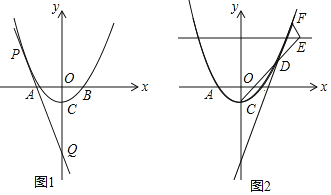
![]() 求c的值;
求c的值;
![]() 是抛物线上一动点,过P点作直线L交y轴于
是抛物线上一动点,过P点作直线L交y轴于![]() ,且直线L和抛物线只有唯一公共点,求
,且直线L和抛物线只有唯一公共点,求![]() 的值;
的值;
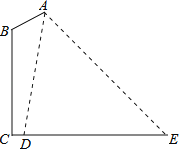
![]() 如图2,E为直线
如图2,E为直线![]() 上的一动点,CE交抛物线于D,
上的一动点,CE交抛物线于D,![]() 轴交抛物线于F,求证:直线FD经过y轴上一定点,并求定点坐标.
轴交抛物线于F,求证:直线FD经过y轴上一定点,并求定点坐标.
【答案】![]() c=-2;
c=-2;![]() ;
;![]() 证明见解析;直线DF恒过点
证明见解析;直线DF恒过点![]() .
.
【解析】
(1)由题意可知:OC=-c,AB=-2c,令y=0代入抛物线的解析式也可求出AB=![]() ,列出方程即可求出c的值;
,列出方程即可求出c的值;
(2)根据P与Q的坐标求出PQ的直线解析式,然后与抛物线联立方程求出△,令△=0后进行化简,即可求出n与s的值;
(3)设E(a,3),F(a,b),然后求出直线CE的解析式,与抛物线联立方程求出D的坐标,最后求出直线DF的解析式即可求出该定点.
(1)由题意可知:![]() ,
,
![]() ,
,
![]() ,
,
令![]() 代入
代入![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 舍去
舍去![]() 或
或![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
(2)设直线PQ的解析式为:![]() ,
,
将![]() 与
与![]() 代入
代入![]() ,
,
可得: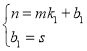 ,
,
解得: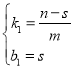 ,
,
![]() 直线PQ的解析式为:
直线PQ的解析式为:![]() ,
,
联立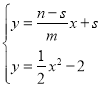 ,
,
化简可得:![]() ,
,
![]() ,
,
![]() 化简可得:
化简可得:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)设![]() ,
,![]() ,
,
设直线CE的解析式为:![]() ,
,
把![]() 和
和![]() 代入
代入![]() ,可得:
,可得: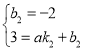 ,
,
解得: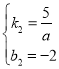 ,
,
![]() 直线CE的解析式为:
直线CE的解析式为:![]() ,
,
![]() 联立
联立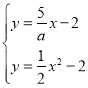 ,
,
解得:![]() 舍去
舍去![]() 或
或![]() ,
,
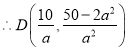 ,
,
设直线DF的解析式为:![]() ,
,
把D和F的坐标分别代入![]() 可得:
可得: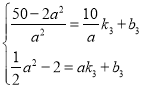 ,
,
解得: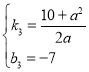 ,
,
![]() 直线DF的解析式为:
直线DF的解析式为:![]() ,
,
令![]() 代入
代入![]() ,
,
![]() ,
,
![]() 直线DF恒过点(0,-7).
直线DF恒过点(0,-7).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目