��Ŀ����
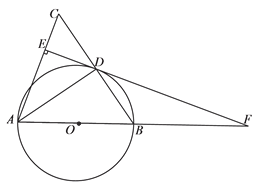
����Ŀ����ͼ����ƽ��ֱ������ϵxoy��������![]() ��x��0����ͼ����ֱ��y=x+2���ڵ�A����3��m����
��x��0����ͼ����ֱ��y=x+2���ڵ�A����3��m����
��1����k��m��ֵ��
��2����֪��P��a��b����ֱ��y=x����λ�ڵ������ĵ�������P��ƽ����x���ֱ������ֱ��y=x+2�ڵ�M������P��ƽ����y���ֱ����������![]() ��x��0����ͼ���ڵ�N��
��x��0����ͼ���ڵ�N��
�ٵ�a=��1ʱ���ж��߶�PM��PN��������ϵ����˵��������
����PN��PM��Ϻ�����ͼ����ֱ��д��b��ȡֵ��Χ��

���𰸡���1��k=3��m=��1����2����PM=PN����-1��b��0��b��-3��
�������������������1����A�����y=x+2�м������m��ֵ��Ȼ��A��������뷴���������м������k��ֵ��
��2���ٵ�a=-1ʱ���ֱ����M��N��������꼴�����PM��PN�Ĺ�ϵ��
���������֪��P������Ϊ��b��b��(b<0)������PN��PM���Ӷ���֪PN��2������ͼ������b�ķ�Χ��
�⣺��1���ߺ���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A��-3��m����
���ڵ�A��-3��m����
��m=-3+2=-1��
��A��-3��-1���� k=-1����-3��=3
��k��ֵ��3��m��ֵ��-1
��2���ٵ�a =-1ʱ���ֵ�P��a��b����ֱ��y=x-2�ϣ�
��P��-1��-1��
��y=-1������![]() ,�ã�x=-3��
,�ã�x=-3��
��M��-3��-1����
PM=2
��x=-1������![]() ����y=-3��
����y=-3��
��N��-1��-3����
��PN=2
��PM=PN
��P��b��b����b<0
��P��ֱ��y=x�ϣ�
����P��ƽ����x���ֱ�ߣ���ֱ��y=x+2�ڵ�M��
M��b+2��b����
��PM=2��
��PN��PM��
��PN��2��
��PN=| ![]() |,
|,
��| ![]() |��2
|��2
��-1��b��0��b��-3

����Ŀ���±��ǼѼ���С�̼Ҵ�;�绰�ļ����շѱ���¼��
�ش��������⣺
ʱ�� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | �� |
�绰�� | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 | �� |
��1���ϱ���ӳ�˱��� �� ֮��Ĺ�ϵ, �Ա����� ,������� .
��2�������Ѽ�Ԥ��һ�£��������绰�õ�ʱ����10���ӣ���Ҫ�� Ԫ�绰�ѣ�
��3������д��ͨ��ʱ��![]() �����ӣ���
�����ӣ���![]() Ϊ������������Ҫ���ĵ绰��
Ϊ������������Ҫ���ĵ绰��![]() ��Ԫ��֮��Ĺ�ϵʽ.
��Ԫ��֮��Ĺ�ϵʽ.