题目内容
探究性问题:
=
-
,
=
-
,
=
-
,则
=______.
试用上面规律解决下面的问题:
(1)计算
+
+
;
(2)已知
+(ab-2)2=0,求
+
+…+
的值.
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
试用上面规律解决下面的问题:
(1)计算
| 1 |
| (x+1)(x+2) |
| 1 |
| (x+2)(x+3) |
| 1 |
| (x+3)(x+4) |
(2)已知
| a-1 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2010)(b+2010) |
根据已知的三个等式,总结规律得
=
-
,
(1)原式=
+
+
=
-
+
-
+
-
=
-
=
;
(2)由
+(ab-2)2=0得:a-1=0且ab-2=0,
解得a=1且ab=2,
所以b=2,
则原式=
+
+…+
,
=
+
+…+
,
=1-
+
-
+
-
+…+
-
+
-
=1-
=
.
故答案为:
-
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(1)原式=
| 1 |
| (x+1)(x+2) |
| 1 |
| (x+2)(x+3) |
| 1 |
| (x+3)(x+4) |
=
| 1 |
| x+1 |
| 1 |
| x+2 |
| 1 |
| x+2 |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 1 |
| x+4 |
| 1 |
| x+1 |
| 1 |
| x+4 |
| 3 |
| (x+1)(x+4) |
(2)由
| a-1 |
解得a=1且ab=2,
所以b=2,
则原式=
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2010)(b+2010) |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2011×2012 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2012 |
| 1 |
| 2012 |
| 2011 |
| 2012 |
故答案为:
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
相关题目
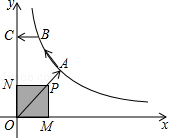
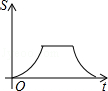 B.
B.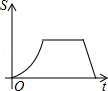 C.
C. D.
D.