题目内容
某超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为每个50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加x元,
(1)写出售出一个可获得的利润是多少元?(用含x的代数式表示)
(2)商店若准备获得利润6 000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(1)写出售出一个可获得的利润是多少元?(用含x的代数式表示)
(2)商店若准备获得利润6 000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
考点:一元二次方程的应用
专题:销售问题
分析:(1)根据利润=销售价-进价列关系式;
(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍;
(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍;
解答:解:(1)由题意得:50+x-40=x+10;
(2)由已知得,(x+10)(400-10x)=6000,
整理得:x2-30x+200=0
解得,x1=10,x2=20,
∵进货量较少,
∴x=20,
进货量为:400-10x=400-200=200.
答:当定价为70元时利润达到6000元,此时的进货量为200个.
(2)由已知得,(x+10)(400-10x)=6000,
整理得:x2-30x+200=0
解得,x1=10,x2=20,
∵进货量较少,
∴x=20,
进货量为:400-10x=400-200=200.
答:当定价为70元时利润达到6000元,此时的进货量为200个.
点评:考查了一元二次方程的应用,应用题中求最值需先求函数表达式,再运用函数性质求解.此题的关键在列式表示销售价格和销售量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各组式子中:①4xyz和7xy;②0.5x2y和0.5xy2;③m2n和nm2,其中是同类项的是( )
| A、① | B、② | C、③ | D、①② |
用四舍五入法得到a的近似数是3.80,精确地说,这个数的范围是( )
| A、3.795≤a<3.805 |
| B、3.75≤a<3.85 |
| C、3.75<a<3.85 |
| D、3.795<a≤3.805 |
 如图,在平面直角坐标系中,直线l与x轴,y轴分别交于A,B两点,且A(4,0),B(0,3).动点P,Q同时从点O出发,点P沿着折线O→B→A匀速运动,点Q沿线段OA匀速运动,两点同时到达点A时,运动停止,已知点Q的运动速度为每秒1个单位长度.
如图,在平面直角坐标系中,直线l与x轴,y轴分别交于A,B两点,且A(4,0),B(0,3).动点P,Q同时从点O出发,点P沿着折线O→B→A匀速运动,点Q沿线段OA匀速运动,两点同时到达点A时,运动停止,已知点Q的运动速度为每秒1个单位长度. 图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.
图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.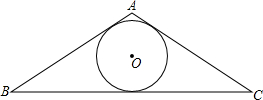 如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.
如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.