题目内容
 图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.
图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:
分析:连EB、EC,根据角平分线性质得EF=EG;根据垂直平分线的性质得EB=EC;再根据“HL”定理证明Rt△EFB≌Rt△EGC,从而得BF=CG.
解答: 答:相等.
答:相等.
证明:连EB、EC,
∵AE是∠BAC的平分线,
且EF⊥AB于F,EG⊥AC于G,
∴EF=EG.
∵ED⊥BC于D,D是BC的中点,
∴EB=EC.
∴Rt△EFB≌Rt△EGC,
∴BF=CG.
 答:相等.
答:相等.证明:连EB、EC,
∵AE是∠BAC的平分线,
且EF⊥AB于F,EG⊥AC于G,
∴EF=EG.
∵ED⊥BC于D,D是BC的中点,
∴EB=EC.
∴Rt△EFB≌Rt△EGC,
∴BF=CG.
点评:本题考查了角平分线性质和垂直平分线的性质,利用了三角形全等的判定和性质解题.正确作出辅助线是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2012年1月有5个星期一,它们的日期和为80,那么这个月中星期六有( )个.
| A、6 | B、5 | C、4 | D、3 |
国家提倡“低碳减排”,某公司计划建风能发电站,电站年均发电量约为258000000度,将数据258000000用科学记数法表示为( )
| A、258×106 |
| B、25.8×107 |
| C、2.58×108 |
| D、2.58×109 |
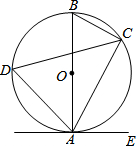 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.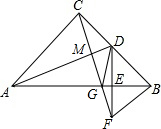 如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.
如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.