题目内容
已知二次函数 与一次函数
与一次函数 的图象交于
的图象交于 和
和 ,则能使
,则能使 成立的
成立的 的取值范围是
的取值范围是

 与一次函数
与一次函数 的图象交于
的图象交于 和
和 ,则能使
,则能使 成立的
成立的 的取值范围是
的取值范围是
A. | B. |
C. | D. 或 或 |
D
试题分析:二次函数
 与一次函数
与一次函数 的图象交于
的图象交于 和
和 ,
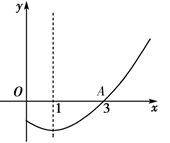
, ,那么从图象上来看就是二次函数的图象要比一次函数的图象高,在本题的图象中即是A点的左边和B点的右边部分,
,那么从图象上来看就是二次函数的图象要比一次函数的图象高,在本题的图象中即是A点的左边和B点的右边部分, 的取值范围为
的取值范围为 或
或
点评:本题考查一次函数和二次函数的图象;要求考生熟练掌握其性质,会通过观察图象求解不等式的解

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
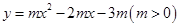 与
与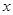 轴交于
轴交于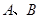 两点,与
两点,与 轴交于
轴交于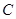 点.
点.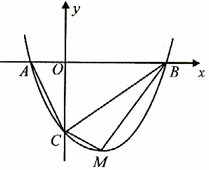
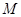 的坐标(用含
的坐标(用含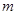 的代数式表示),
的代数式表示),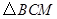 与
与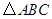 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值; 年的维修、保养费用累计为
年的维修、保养费用累计为 (万元),且
(万元),且 ,若第1年的维修、保养费用为2万元,第2年为4万元。
,若第1年的维修、保养费用为2万元,第2年为4万元。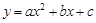 ,使它同时具有如下性质:
,使它同时具有如下性质: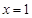 对称;②当x=2时,y>0;③当x=-2时,y<0.
对称;②当x=2时,y>0;③当x=-2时,y<0.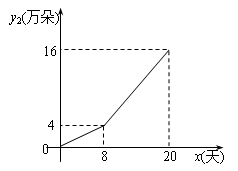
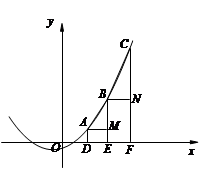
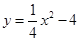 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
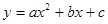 图象的一部分,其对称轴为
图象的一部分,其对称轴为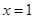 ,若其与x轴一交点为A(3,0),则有图象可知不等式
,若其与x轴一交点为A(3,0),则有图象可知不等式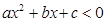 的解集是____________.
的解集是____________.