题目内容
如图,在直角坐标系x O y中,二次函数 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.

(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图像上,且∠DAC = 45°,求点D的坐标.
 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
(1)求这个二次函数的解析式;
(2)求∠BAC的正切值;
(3)如果点D在这个二次函数的图像上,且∠DAC = 45°,求点D的坐标.
(1)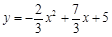 (2)
(2)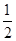 (3)
(3)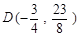
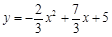 (2)
(2)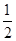 (3)
(3)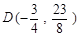
试题分析:解:(1)∵ 二次函数
 的图像经过点A(5,0),
的图像经过点A(5,0),∴
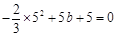 .
.解得
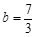 .
. ∴ 二次函数的解析式是
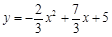
(2)当 x = 0时,得 y = 5.∴ B(0,5).
当 x = 3时,得
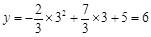 ,∴ C(3,6).
,∴ C(3,6).联结BC.
∵
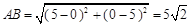 ,
,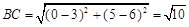 ,
,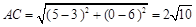 ,
,∴
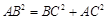 .
.∴
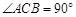 .
.∴
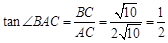 .
.(3)设D(m,n).
过点D作DE⊥x轴,垂足为点E.则
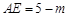 ,DE = n.
,DE = n.∵ A(5,0),B(0,5),∴ OA = OB.
又∵
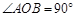 ,∴
,∴ 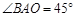 ,
,即得 ∠DAE +∠BAD = 45º.
又∵ ∠DAC = 45º,即 ∠BAD +∠BAC = 45º,
∴ ∠DAE =∠BAC.
又∵ ∠DEA =∠ACB = 90º,
∴ △DAE∽△BAC.
∴
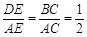 .
.∴
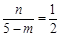 .即得
.即得 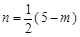 .
.∵ 点D在二次函数
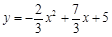 的图像上,
的图像上,∴
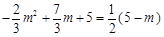 .
.解得
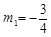 ,m2 = 5(不合题意,舍去).
,m2 = 5(不合题意,舍去).∴
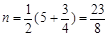 .
.∴
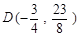 .
.点评:该题是常考题,将二次函数的图像和二次函数值联系在一起,考查学生对二次函数的系数和三角函数值的求解方法,要求学生必须掌握。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且
与y轴交于点C,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且 .点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作
.点E为线段BC上的动点(点E不与点B,C重合),以E为顶点作 ,射线ET交线段OB于点F.
,射线ET交线段OB于点F.
 ;
; 为等腰三角形时,求此时点E的坐标;
为等腰三角形时,求此时点E的坐标;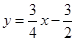 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.



 的开口方向向下,那么a的取值范围是 .
的开口方向向下,那么a的取值范围是 . 与一次函数
与一次函数 的图象交于
的图象交于 和
和 ,则能使
,则能使 成立的
成立的 的取值范围是
的取值范围是



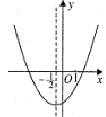
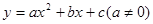 的图象如图所示对称轴为x=-1/2。
的图象如图所示对称轴为x=-1/2。