题目内容
4. 如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.
如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.(1)请写出点C,D的坐标;
(2)求四边形ABDC的面积;
(3)在x轴上求作一点P,使PA+PB的值最小(保留作图痕迹,不要求写作法),并直接写出点P坐标.
分析 (1)关于y轴对称的两点的横坐标互为相反数,纵坐标相等;
(2)利用梯形的面积公式计算即可;
(3)首先求得点A关于x轴的对称点A′,连接A′B交x轴于点P,此时PA+PB的值最小.
解答 解:(1)点C的坐标为(-2,3),点D的坐标为(-6,1);
(2)四边形ABDC的面积=$\frac{1}{2}×2×(4+12)$=16;
(3)如图所示:
根据图形可知点P的坐标为(5,0).
点评 本题主要考查的是轴对称图形的性质、梯形的面积公式、轴对称--路径最短问题,掌握轴对称图形的性质是解题的关键.

练习册系列答案
相关题目
19.如图放置的四个几何体中,主视图是圆形的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |


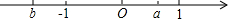 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.