题目内容
8. 如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则(1)$\frac{AB}{AC}$的值是$\sqrt{2}$;(2)$\frac{BF}{EF}$的值是$\sqrt{2}+1$.
如图,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD、AC于点E,F,则(1)$\frac{AB}{AC}$的值是$\sqrt{2}$;(2)$\frac{BF}{EF}$的值是$\sqrt{2}+1$.
分析 作FG⊥AB于点G,由AE∥FG,得出$\frac{BF}{EF}=\frac{BG}{GA}$,求出Rt△BGF≌Rt△BCF,再由AB=$\sqrt{2}$BC求解.
解答  解:作FG⊥AB于点G,
解:作FG⊥AB于点G,
∵∠DAB=90°,
∴AE∥FG,
∴$\frac{BF}{EF}=\frac{BG}{GA}$,
∵AC⊥BC,
∴∠ACB=90°,
又∵BE是∠ABC的平分线,
∴FG=FC,
在Rt△BGF和Rt△BCF中,
$\left\{\begin{array}{l}{BF=BF}\\{CF=GF}\end{array}\right.$,
∴Rt△BGF≌Rt△BCF(HL),
∴CB=GB,
∵AC=BC,
∴∠CBA=45°,
∴AB=$\sqrt{2}$BC=$\sqrt{2}$AC,
∴$\frac{AB}{AC}=\sqrt{2}$,
∴$\frac{BF}{EF}=\frac{BG}{GA}$=$\frac{BC}{\sqrt{2}BC-BC}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1.
故答案为:$\sqrt{2}$,$\sqrt{2}+1$.
点评 本题主要考查了平行线分线段成比例,全等三角形的判定与性质及角平分线的知识,解题的关键是找出线段之间的关系:CB=GB,AB=$\sqrt{2}$BC,再利用比例式求解.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
20.明明借助一副三角尺和量角器,先画∠AOB=90°,再以点O为顶点,OB为始边,作∠BOC=30°,最后作∠AOC的平分线OD,则∠COD的度数为( )
| A. | 30° | B. | 60° | C. | 30°或60° | D. | 15°或45° |
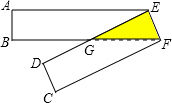 点E、F分别在一张长方形纸条ABCD的边AD、BC上,将这张纸条沿着直线EF对折后如图,BF与DE交于点G,如果∠BGD=30°,长方形纸条的宽AB=3cm,那么这张纸条对折后的重叠部分面积S△GEF=9cm2.
点E、F分别在一张长方形纸条ABCD的边AD、BC上,将这张纸条沿着直线EF对折后如图,BF与DE交于点G,如果∠BGD=30°,长方形纸条的宽AB=3cm,那么这张纸条对折后的重叠部分面积S△GEF=9cm2. 如图,已知△ABC,用尺规作图作出BC边上的高AD(保留作图痕迹,不写作法),
如图,已知△ABC,用尺规作图作出BC边上的高AD(保留作图痕迹,不写作法),