Question

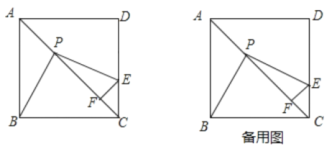
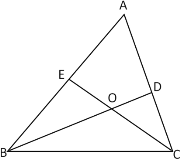
【题目】如图所示，已知中，，BD、CE分别平分和，BD、CE交于点O．

求证：BE+CD=BC．

Answer 1

【答案】见解析.

【解析】

在BC上取点G使得CG＝CD，可证△COD≌△COG，得∠BOG＝∠BOE，然后证△BOE≌△BOG，得BE＝BG，可以求得BE＋CD＝BC．

解：在BC上取点G使得CG＝CD，

∵∠BOC＝180°（∠ABC＋∠ACB）＝180°（180°60°）＝120°，

∴∠BOE＝∠COD＝60°，

∵在△COD和△COG中，，

∴△COD≌△COG（SAS），

∴∠COG＝∠COD＝60°，

∴∠BOG＝120°60°＝60°＝∠BOE，

∵在△BOE和△BOG中，，

∴△BOE≌△BOG（ASA），

∴BE＝BG，

∴BE＋CD＝BG＋CG＝BC．