Question

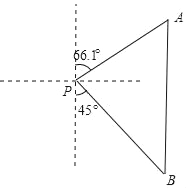
【题目】如图，一艘海轮位于灯塔P的北偏东66.1°方向，距离灯塔120海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求BP和BA的长（结果取整数）．

参考数据：sin66.1°≈0.91，cos66.1°≈0.41，tan64°≈2.26，取1.414．

Answer 1

【答案】BP的长为154海里，BA的长为158海里．

【解析】分析：如图作PC⊥AB于C．在Rt△APC中，求出PC、AC的长，在Rt△PCB中求出PB的长，从而可解决问题．

详解：如图作PC⊥AB于C．

由题意∠A=66.1°，∠B=45°，PA=120，

在Rt△APC中，sinA=，cosA=，

∴PC=PAsinA=120sin66.1°，

AC=PAcosA=120cos66.1°，

在Rt△PCB中，∵∠B=45°，

∴PC=BC，

∴PB==≈154．

∴AB=AC+BC=120cos66.1°+120sin66.1°

≈120×0.41+120×0.91

≈158．

答：BP的长为154海里和BA的长为158海里．