题目内容
【题目】如图,过![]() 轴正半轴上的任意一点
轴正半轴上的任意一点![]() ,作
,作![]() 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于点
的图象交于点![]() 和点
和点![]() ,点
,点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3B. 4C. 5D. 6
【答案】A
【解析】
设P(0,b),由直线AB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数![]() 和
和![]() 的图象上,可得A点坐标为(-
的图象上,可得A点坐标为(-![]() ,b),B点坐标为(
,b),B点坐标为(![]() ,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,
∵点A在反比例函数![]() 的图象上,
的图象上,
∴当y=b,x=-![]() ,即A点坐标为(-
,即A点坐标为(-![]() ,b),
,b),
又∵点B在反比例函数![]() 的图象上,
的图象上,
∴当y=b,x=![]() ,即B点坐标为(
,即B点坐标为(![]() ,b),
,b),
∴AB=![]() -(-
-(-![]() )=
)=![]() ,
,
∴S△ABC=![]() ABOP=
ABOP=![]()
![]() b=3.
b=3.
故选A.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】如图7所示,点![]() 、
、![]() 、
、![]() 在
在![]() 轴上,且
轴上,且![]() ,分别过点
,分别过点![]() 、
、![]() 、
、![]() 作
作![]() 轴的平行线,与反比例函数
轴的平行线,与反比例函数![]() 的图象分别交于点
的图象分别交于点![]() 、
、![]() 、
、![]() ,分别过点
,分别过点![]()
![]()
![]() 作
作![]() 轴的平行线,分别与
轴的平行线,分别与![]() 轴交于点
轴交于点![]()
![]()
![]() ,连接
,连接![]()
![]()
![]() ,那么图中阴影部分的面积之和为___________.
,那么图中阴影部分的面积之和为___________.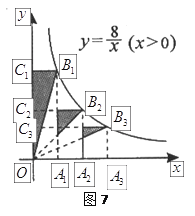
【题目】观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,完成下列题目:
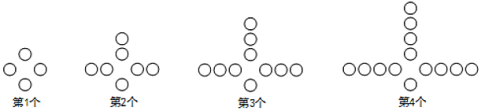
(1)填写下表:
图案序号 | 1 | 2 | 3 | 4 | … |
|
○个数 | 4 | 7 | … |
(2)若按上面的规律继续摆放,是否存在第![]() 个图形,其中恰好含有2020个○?
个图形,其中恰好含有2020个○?