题目内容
16. 已知:A(0,1),B(2,0),C(4,3)
已知:A(0,1),B(2,0),C(4,3)(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
分析 (1)确定出点A、B、C的位置,连接AC、CB、AB即可;
(2)过点C向x、y轴作垂线,垂足为D、E,△ABC的面积=四边形DOEC的面积-△ACE的面积-△BCD的面积-△AOB的面积;
(3)当点p在x轴上时,由△ABP的面积=4,求得:BP=8,故此点P的坐标为(10,0)或(-6,0);当点P在y轴上时,△ABP的面积=4,解得:AP=4.所以点P的坐标为(0,5)或(0,-3).
解答 解:(1)如图所示:
(2)过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积=$\frac{1}{2}×2×3$=3,△ACE的面积=$\frac{1}{2}×2×4$=4,△AOB的面积=$\frac{1}{2}×2×1$=1.
∴△ABC的面积=四边形DOEC的面积-△ACE的面积-△BCD的面积-△AOB的面积
=12-3-4-1=4.
当点p在x轴上时,△ABP的面积=$\frac{1}{2}AO•BP$=4,即:$\frac{1}{2}×1×BP=4$,解得:BP=8,
所点P的坐标为(10,0)或(-6,0);
当点P在y轴上时,△ABP的面积=$\frac{1}{2}×BO×AP$=4,即$\frac{1}{2}×2×AP=4$,解得:AP=4.
所以点P的坐标为(0,5)或(0,-3).
所以点P的坐标为(0,5)或(0,-3)或(10,0)或(-6,0).
点评 本题主要考查的是点的坐标与图形的性质,明确△ABC的面积=四边形DOEC的面积-△ACE的面积-△BCD的面积-△AOB的面积是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
4.下列事件是随机事件的是( )
| A. | 购买一张福利彩票中奖 | |
| B. | 400人中至少有两人的生日在同一天 | |
| C. | 有一名运动员奔跑的速度是30米/秒 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
1.下列运算中正确的是( )
| A. | (a3)2=a5 | B. | a2+a3=a5 | C. | (a+1)2=a2+1 | D. | a5÷a3=a2 |
5.若二次函数y1=a1x2-1与二次函数y2=a2x2+3图象的形状完全相同,则a1与a2的关系为( )
| A. | a1=a2 | B. | a1=-a2 | C. | a1=±a2 | D. | 无法判断 |

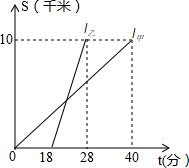 某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
某中学甲、乙两位教师先后从学校出发,到距学校10km的培训中心参加新教材培训学习,图中I甲,I乙分别表示甲、乙两位教师从学校到培训中心所走的路程S(km)随时间t(分钟)变化的函数图象.
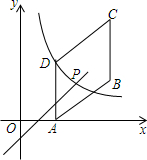 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.