题目内容
18.在平面直角坐标系中,O为坐标原点,点A在第二象限,点B在x轴负半轴上,△OAB的面积是9,P是AB中点,若函数$y=\frac{k}{x}$(x<0)的图象经过点A、P,则k的值为( )| A. | -6 | B. | -4 | C. | -3 | D. | -2 |
分析 设点A坐标为(m,n),点B(a,0),根据三角形面积公式得到-$\frac{1}{2}$an=9,即an=-9,再根据线段中点坐标公式得到点P坐标为($\frac{m+a}{2}$,$\frac{n}{2}$),接着根据反比例函数图象上点的坐标特征得到k=$\frac{m+a}{2}$•$\frac{n}{2}$=mn,然后通过计算可得k=-6.
解答 解:设点A坐标为(m,n),点B(a,0),
∵S△OAB=9,
∴-$\frac{1}{2}$an=9,
∵P是AB的中点,
∴点P坐标为($\frac{m+a}{2}$,$\frac{n}{2}$),
而函数$y=\frac{k}{x}$(x<0)的图象经过点A、P,
∴k=$\frac{m+a}{2}$•$\frac{n}{2}$=mn,
∴3mn=an,
∵-an=18,
∴mn=-6
∴k=-6.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
9.三边均为整数,且最大边长为11的三角形共有( )个.
| A. | 20 | B. | 26 | C. | 30 | D. | 36 |
8.若化简|2-x|-$\sqrt{{x}^{2}-8x+16}$的结果是-2,则x的取值范围是( )
| A. | x为任意实数 | B. | 2≤x≤4 | C. | x≥4 | D. | x≤2 |
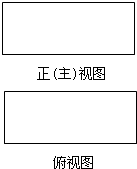 如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )
如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )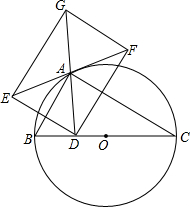 如图,点A在以BC为直径的半圆上,BC=8,∠ACB=30°,点D在线段BC上运动,点E与点D关于AB对称,点F与点D关于AC对称,点G与点D关于点A对称.连结DE、EG、GF、FD、EF、GD,则:
如图,点A在以BC为直径的半圆上,BC=8,∠ACB=30°,点D在线段BC上运动,点E与点D关于AB对称,点F与点D关于AC对称,点G与点D关于点A对称.连结DE、EG、GF、FD、EF、GD,则: