题目内容
 如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为
如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为考点:二次函数综合题
专题:压轴题
分析:连接OB,根据正方形的对角线平分一组对角线可得∠BOC=45°,过点B作BD⊥x轴于D,然后求出∠BOD=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得BD=
OB,再利用勾股定理列式求出OD,从而得到点B的坐标,再把点B的坐标代入抛物线解析式求解即可.
| 1 |
| 2 |
解答: 解:如图,连接OB,
解:如图,连接OB,
∵四边形OABC是边长为1的正方形,
∴∠BOC=45°,OB=1×
=
,
过点B作BD⊥x轴于D,
∵OC与x轴正半轴的夹角为15°,
∴∠BOD=45°-15°=30°,
∴BD=
OB=
,
OD=
=
,
∴点B的坐标为(
,-
),
∵点B在抛物线y=ax2(a<0)的图象上,
∴a(
)2=-
,
解得a=-
.
故答案为:-
.
 解:如图,连接OB,
解:如图,连接OB,∵四边形OABC是边长为1的正方形,
∴∠BOC=45°,OB=1×
| 2 |
| 2 |
过点B作BD⊥x轴于D,
∵OC与x轴正半轴的夹角为15°,
∴∠BOD=45°-15°=30°,
∴BD=
| 1 |
| 2 |
| ||
| 2 |
OD=
(
|
| ||
| 2 |
∴点B的坐标为(
| ||
| 2 |
| ||
| 2 |
∵点B在抛物线y=ax2(a<0)的图象上,
∴a(
| ||
| 2 |
| ||
| 2 |
解得a=-
| ||
| 3 |
故答案为:-
| ||
| 3 |
点评:本题是二次函数综合题型,主要利用了正方形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,二次函数图象上点的坐标特征,熟记正方形性质并求出OB与x轴的夹角为30°,然后求出点B的坐标是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
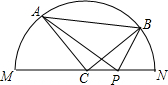 如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若
如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若 |
| MA |
 |
| BN |
| A、10° | B、15° |
| C、20° | D、25° |

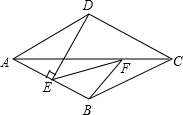 如图,在边长为6的菱形ABCD中,DE⊥AB于点E,并且点E是AB的中点,点F在线段AC上运动,则EF+FB的最小值是
如图,在边长为6的菱形ABCD中,DE⊥AB于点E,并且点E是AB的中点,点F在线段AC上运动,则EF+FB的最小值是