题目内容
3.已知a=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,b=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,求$\frac{b}{a}$+$\frac{a}{b}$的值.分析 把a,b的值代入代数式,根据二次根式的性质化简,即可解答.
解答 解:$\frac{b}{a}+\frac{a}{b}$
=($\frac{\sqrt{2}+1}{\sqrt{2}-1}$÷$\frac{\sqrt{2}-1}{\sqrt{2}+1}$)+($\frac{\sqrt{2}-1}{\sqrt{2}+1}$÷$\frac{\sqrt{2}+1}{\sqrt{2}-1}$)
=$\frac{\sqrt{2}+1}{\sqrt{2}-1}×\frac{\sqrt{2}+1}{\sqrt{2}-1}$+$\frac{\sqrt{2}-1}{\sqrt{2}+1}×\frac{\sqrt{2}-1}{\sqrt{2}+1}$
=$\frac{3+2\sqrt{2}}{3-2\sqrt{2}}$+$\frac{3-2\sqrt{2}}{3+2\sqrt{2}}$
=$\frac{(3+2\sqrt{2})^{2}-(3-2\sqrt{2})^{2}}{(3-2\sqrt{2})(3+2\sqrt{2})}$
=$\frac{9+12\sqrt{2}+8-9+12\sqrt{2}-8}{9-8}$
=24$\sqrt{2}$.
点评 本题考查了二次根式的化简求值,解决本题的关键是熟记二次根式的乘除.

练习册系列答案
相关题目
13.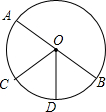 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
 如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )
如图,AB是⊙O的直径,$\widehat{BD}$=$\widehat{CD}$,∠BOD=60°,则∠AOC=( )| A. | 30° | B. | 45° | C. | 60° | D. | 以上都不正确 |
9.与$\sqrt{2}$是同类二次根式的为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{24}$ |
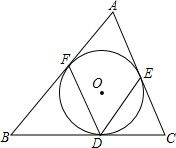 如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.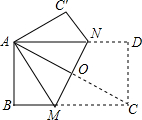 如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.
如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.