题目内容
9.与$\sqrt{2}$是同类二次根式的为( )| A. | $\sqrt{6}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{24}$ |
分析 先化简,再根据同类二次根式的定义解答.
解答 解:A、$\sqrt{6}$与$\sqrt{2}$被开方数不同,故A错误;
B、$\sqrt{8}$=2$\sqrt{2}$与$\sqrt{2}$被开方数相同,故B正确;
C、$\sqrt{12}$=2$\sqrt{3}$与$\sqrt{2}$的被开方数不同,故C错误;
D、$\sqrt{24}$=2$\sqrt{6}$与$\sqrt{2}$被开方数不同,故D错误;
故选:B.
点评 此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列不等式中,是一元一次不等式的是( )
| A. | 2(1-y)+y>4y+2 | B. | x(x-5)≥4 | C. | $\frac{1}{2}-\frac{1}{4}>\frac{1}{5}$ | D. | y+1<y+2 |
17.在Rt△ABC中,∠C=90°,则下列等式成立的是( )
| A. | AB=AC×sinB | B. | BC=AB×sinB | C. | BC=AC×tanB | D. | BC=AC×tanA |
4.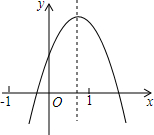 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④b2-4ac>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④b2-4ac>0,其中正确结论的个数为( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④b2-4ac>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③4a-2b+c<0;④b2-4ac>0,其中正确结论的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1.在10张奖券中,有4张有奖,从中任抽一张,能中奖的概率为( )
| A. | $\frac{4}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
19.下列关于x的方程中,没有实数根的是( )
| A. | 3x2+4x-2=0 | B. | 2x2+5=6x | C. | 3x2-2$\sqrt{6}$x+2=0 | D. | 2x2+mx-1=0 |